Question

袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为.现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.

(1)求袋中原有白球的个数，

(2)求取球2次终止的概率；

(3)求甲取到白球的概率.

Answer 1

解：(1)设袋中原有n个白球，由题意，知

,

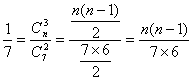∴n(n-1)=6.解得n=3(舍去n=-2),即袋中原有3个白球.

(2)记“取球2次终止”的事件为A，则P(A)=.

(3)因为甲先取，所以甲只有可能在第1次、第3次和第5次取球，记“甲取到白球”的事件为A，

    则P(A)=P(“ξ=1”，或“ξ=3”，或“ξ=5”).

    因为事件“ξ=1”“ξ=3”“ξ=5”两两互斥，所以

P(A)=P(ξ=1)+P(ξ=3)+P(ξ=5)=.