题目内容
△ABC中,角A、B、C所对应的边分别为a,b,c,若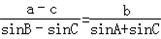 .
.
(1)求角A;
(2)若函数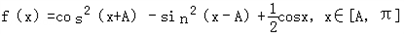 ,
,
求函数f(x)的值域.
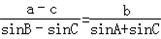 .
. (1)求角A;
(2)若函数
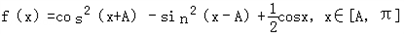 ,
,求函数f(x)的值域.
解:(1)由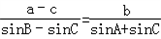 ,以及正弦定理,
,以及正弦定理,
可得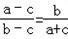 ,即a2=b2+c2﹣bc,
,即a2=b2+c2﹣bc,
由余弦定理可知cosA= ,
,
因为A是三角形内角,
所以A=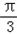 .
.
(2)由(1)可知,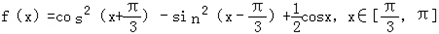
∴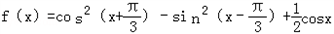
=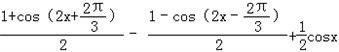
=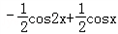
=﹣cos2x+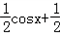
=﹣t2+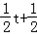
其中t=cosx,
∵x∈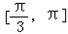 ,
,
∴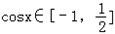 .
.
当t=﹣1时,f小(x)=﹣1,
当t= 时,f大(x)=
时,f大(x)=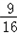 ,
,
∴函数f(x)的值域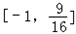 .
.
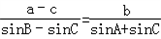 ,以及正弦定理,
,以及正弦定理,可得
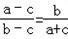 ,即a2=b2+c2﹣bc,
,即a2=b2+c2﹣bc,由余弦定理可知cosA=
 ,
,因为A是三角形内角,
所以A=
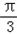 .
.(2)由(1)可知,
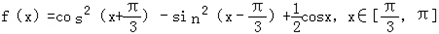
∴
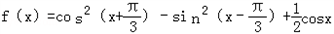
=
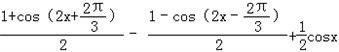
=
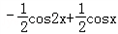
=﹣cos2x+
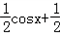
=﹣t2+
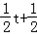
其中t=cosx,
∵x∈
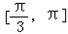 ,
,∴
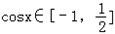 .
.当t=﹣1时,f小(x)=﹣1,
当t=
 时,f大(x)=
时,f大(x)=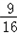 ,
,∴函数f(x)的值域
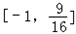 .
.
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目