题目内容
已知函数 在区间
在区间 内任取两个实数
内任取两个实数 ,且
,且 ,
,
不等式 恒成立,则实数
恒成立,则实数 的取值范围为 .
的取值范围为 .

解析试题分析:因为 ,不妨设
,不妨设 ,
,


因为 ,所以
,所以 ,所以
,所以 在
在 内是增函数,所以
内是增函数,所以 在
在 内恒成立,即
内恒成立,即 恒成立,所以
恒成立,所以 的最大值,因为
的最大值,因为 在
在 上的最大值为
上的最大值为 ,所以实数
,所以实数 的取值范围为
的取值范围为 .
.
考点:本小题主要考查函数单调性的应用、利用导数研究函数的单调性和恒成立问题,考查学生灵活运用定义的能力和转化问题的能力以及运算求解能力.
点评:解决此小题的关键在于将已知条件转化为单调性问题,用导数研究单调性又转化为恒成立问题,而恒成立问题又往往转化为最值问题来解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则不等式
,则不等式 的解集是
的解集是  ,且
,且 ,则
,则 .
. ,恒有“当
,恒有“当 时,都存在
时,都存在 满足方程
满足方程 ”,则实数
”,则实数 的取值构成的集合为 .
的取值构成的集合为 . ;
; 则
则
 (
(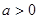 且
且 ,且
,且 ,则
,则 的取值范围是
的取值范围是  的解为________.
的解为________. ,若a <b,且f(a)=f(b),则a+2b的取值范围是________ .
,若a <b,且f(a)=f(b),则a+2b的取值范围是________ .