题目内容
(本题10分)已知函数 ,在区间
,在区间 上有最大值4、最小值1,设函数
上有最大值4、最小值1,设函数 。
。
(1)求 、
、 的值;
的值;
(2)若不等式 在
在 上恒成立,求
上恒成立,求 的取值范围。
的取值范围。
【答案】
(1) 。 (2)
。 (2) 。
。
【解析】本试题主要是考查了二次函数的最值问题和不等式恒成立问题的运用。
(1)函数 ,在区间
,在区间 上有最大值4、最小值1,可知参数a的值。
上有最大值4、最小值1,可知参数a的值。
(2)由(1)知:
所以
因为 ,所以
,所以
 ,进而得到范围。
,进而得到范围。
解:(1)由于函数 的对称轴为直线
的对称轴为直线 ,
, ,所以
,所以 在
在 单调递增,
单调递增,
则 ,解得:
,解得: 。(4分)
。(4分)
(2)由(1)知:
所以 (6分)
(6分)
因为 ,所以
,所以
 ,
,
所以 的最小值为0。(9分)
的最小值为0。(9分)
所以 (10分)
(10分)

练习册系列答案
相关题目
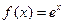 (
(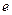 是自然对数的底数,
是自然对数的底数,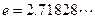 ).
).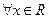 ,不等式
,不等式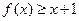 恒成立;
恒成立;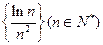 的前
的前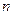 项和为
项和为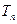 ,求证:
,求证: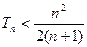 .
. (本题10分)
(本题10分)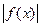 <6的解集为
<6的解集为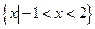 ,试求不等式
,试求不等式 ≤1的解集.
≤1的解集. 时都取得极值.(1)求
时都取得极值.(1)求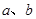 的值;
的值;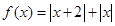
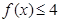 ;
;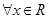 ,恒有
,恒有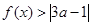 成立,求
成立,求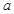 的取值范围.
的取值范围.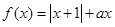 (
(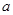 ∈R).
∈R).