Question

(本小题满分12分)

如图，四棱柱ABCD—A₁B₁C₁D₁的底面边长和侧棱长都等于2，平面A₁ACC₁⊥平面ABCD，∠ABC＝∠A₁AC＝60°，点O为底面对角线AC与BD的交点.

  （Ⅰ）证明：A₁O⊥平面ABCD；

  （Ⅱ）求二面角D—A₁A—C的平面角的正切值.

 

Answer 1

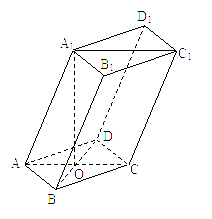（1）见解析（2）2

解析:

（Ⅰ）由已知AB＝BC＝2，∠ABC＝60°，则

△ABC为正三角形，所以AC＝2.                                               （2分）

因为点O为AC的中点，则AO＝1.

又AA₁＝2，∠A₁AO＝60°，

在△A₁OA中，由余弦定理，得

.                                    （4分）

所以A₁O²＋AO²＝AA₁²，所以A₁O⊥AC.                                    （5分）

因为平面AA₁C_??1C⊥平面ABCD，其交线为AC，

所以A₁O⊥平面ABCD.                                               （6分）

（Ⅱ）因为底面ABCD为菱形，则BD⊥AC.又BD⊥A₁O，则BD⊥平面A₁ACC₁.      （7分）

过点O作OE⊥AA₁垂足为E，连接DE，则AA₁⊥DE，

所以∠DEO为二面角D－AA₁－C的平面角.                                   （9分）

在Rt△AOD中，OD=.                                    （10分）

在Rt△AEO中，OE＝AO·sin∠EAO＝.                                  （11分）

在Rt△DOE中，tan∠DEO＝.

故二面角D—A₁A—C的平面角的正切值为2.                     （12分）