题目内容
已知函数y=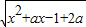
的值域为[0，+∞），则a的取值范围是 ．
【答案】分析：令t=g（x）=x2+ax-1+2a，由题意可得a2-4（2a-1）≥0，解此一元二次不等式，求得a的取值范围．
解答：解：令t=g（x）=x2+ax-1+2a，要使函数
的值域为[0，+∞），
则说明[0，+∞）⊆{y|y=g（x）}，即二次函数的判别式△≥0，
即a2-4（2a-1）≥0，即a2-8a+4≥0，解得
或
，
所以a的取值范围是{a|
，或
}，
故答案为 {a|
，或
}．
点评：本题主要考查函数的值域的应用，二次函数的性质，体现了转化的数学思想，属于基础题．
解答：解：令t=g（x）=x2+ax-1+2a，要使函数
的值域为[0，+∞），则说明[0，+∞）⊆{y|y=g（x）}，即二次函数的判别式△≥0，
即a2-4（2a-1）≥0，即a2-8a+4≥0，解得
或，所以a的取值范围是{a|
，或}，故答案为 {a|
，或}．点评：本题主要考查函数的值域的应用，二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
的值域为［－1，4］，求实数a、b的值.
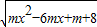的定义域为R．
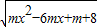的定义域为R．
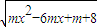的定义域为R．