题目内容
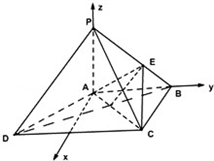
如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
(Ⅰ)当PD∥平面EAC时,确定点E在棱PB上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角A﹣CE﹣P余弦值.
(Ⅰ)当PD∥平面EAC时,确定点E在棱PB上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角A﹣CE﹣P余弦值.
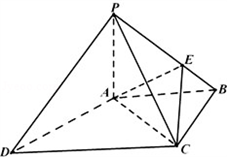
解:(Ⅰ)在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=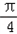 ,
,
∴∠DCA=∠BAC=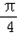 .又AC⊥AD,故△DAC为等腰直角三角形.
.又AC⊥AD,故△DAC为等腰直角三角形.
∴DC=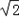 AC=
AC=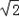 (
(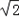 AB)=2AB.
AB)=2AB.
连接BD,交AC于点M,则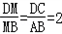
∵PD∥平面EAC,又平面EAC∩平面PDB=ME,∴PD∥EM
在△BPD中,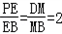 ,
,
即PE=2EB时,PD∥平面EAC
(Ⅱ)以A为原点,AB,AP所在直线分别为y轴、z轴,
如图1建立空间直角坐标系.
设PA=AB=BC=a,
则A(0,0,0),B(0,a,0),C(a,a,0),P(0,0,a),E(0,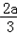 ,).
,).
设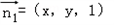 ,为平面EAC的一个法向量,
,为平面EAC的一个法向量,
则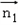 ⊥
⊥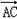 ,
,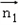 ⊥
⊥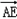 ,
,
∴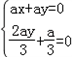 ,解得x=
,解得x= ,y=﹣
,y=﹣ ,
,
∴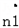 =(
=( ,﹣
,﹣ ,1).
,1).
设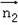 =(
=( ,
, ,1)为平面PBC的一个法向量,
,1)为平面PBC的一个法向量,
则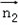 ⊥
⊥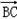 ,
,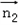 ⊥
⊥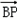 ,
,
又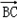 =(a,0,0),
=(a,0,0),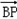 =(0,﹣a,a),
=(0,﹣a,a),
∴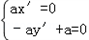 ,解得x'=0,y'=1,
,解得x'=0,y'=1,
∴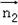 =(0,1,1).∴cos
=(0,1,1).∴cos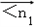 ,
,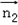 >
>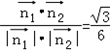
∴二面角A﹣CE﹣P的余弦值为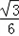
.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=