题目内容
若函数f(x)=|nx-2|,(n∈R,n≠0)的图象的对称轴为x=2,则n=________.
1
分析:化简函数为f(x)=|nx-2|=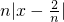 ,它的图象应该是偶函数y=n|x|向右平移
,它的图象应该是偶函数y=n|x|向右平移 个单位而得,故对称轴应该是x=
个单位而得,故对称轴应该是x= ,再对照已知条件得
,再对照已知条件得 =2,可得n=1.
=2,可得n=1.
解答:根据题意,得f(x)=|nx-2|=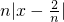 ,
,
可见函数的原型是偶函数y=n|x|,
而函数y=n|x|向右平移 个单位可得y=
个单位可得y=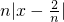 =|nx-2|,即为原函数
=|nx-2|,即为原函数
根据偶函数图象关于y轴对称,可知本题中函数图象关于直线x= 对称,
对称,
∵函数f(x)=|nx-2|,(n∈R,n≠0)的图象的对称轴为x=2
∴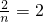 ?n=1
?n=1
故答案为1
点评:本题以含有绝对值的函数为例,考查了函数图象及函数图象的变化,属于中档题.巧妙利用偶函数图象关于y轴对称,找到函数的原型加以解决,是本题的关键.
分析:化简函数为f(x)=|nx-2|=
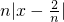 ,它的图象应该是偶函数y=n|x|向右平移
,它的图象应该是偶函数y=n|x|向右平移 个单位而得,故对称轴应该是x=
个单位而得,故对称轴应该是x= ,再对照已知条件得
,再对照已知条件得 =2,可得n=1.
=2,可得n=1.解答:根据题意,得f(x)=|nx-2|=
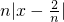 ,
,可见函数的原型是偶函数y=n|x|,
而函数y=n|x|向右平移
 个单位可得y=
个单位可得y=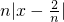 =|nx-2|,即为原函数
=|nx-2|,即为原函数根据偶函数图象关于y轴对称,可知本题中函数图象关于直线x=
 对称,
对称,∵函数f(x)=|nx-2|,(n∈R,n≠0)的图象的对称轴为x=2
∴
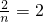 ?n=1
?n=1故答案为1
点评:本题以含有绝对值的函数为例,考查了函数图象及函数图象的变化,属于中档题.巧妙利用偶函数图象关于y轴对称,找到函数的原型加以解决,是本题的关键.

练习册系列答案
相关题目