题目内容
已知双曲线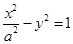
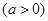 的一个焦点与抛物线
的一个焦点与抛物线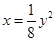 的焦点重合,则此双曲线的离心率为( )
的焦点重合,则此双曲线的离心率为( )
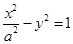
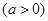 的一个焦点与抛物线
的一个焦点与抛物线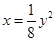 的焦点重合,则此双曲线的离心率为( )
的焦点重合,则此双曲线的离心率为( )A.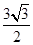 | B.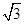 | C.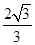 | D. |
C
试题分析:先确定抛物线的焦点坐标,可得双曲线的焦点坐标,从而可求双曲线的离心率.解:抛物线y2=8x的焦点坐标为(2,0),∵抛物线y2=8x的焦点与双曲线
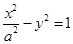
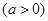 的一个焦点重合,可知∴a2+1=4,∴a=
的一个焦点重合,可知∴a2+1=4,∴a=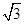 ,故可知双曲线的离心率为
,故可知双曲线的离心率为 ,故选C.
,故选C.点评:本题考查抛物线的标准方程,考查抛物线与双曲线的几何性质,属于基础题

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
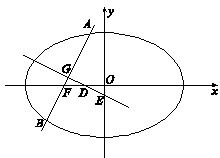
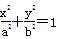 (a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=
(a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=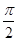 ,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1∶2,则该椭圆的离心率等于
,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1∶2,则该椭圆的离心率等于 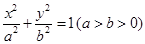 的左焦点为
的左焦点为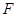 ,过点
,过点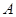 ,
,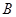 两点.当直线
两点.当直线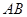 经过椭圆的一个顶点时,其倾斜角恰为
经过椭圆的一个顶点时,其倾斜角恰为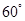 .
.
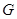 ,
,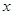 轴和
轴和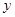 轴分别交于
轴分别交于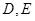 两点,
两点,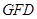 的面积为
的面积为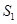 ,△
,△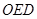 (
(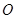 为原点)的面积为
为原点)的面积为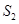 ,求
,求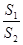 的取值范围.
的取值范围.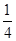



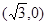
 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且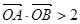 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围.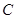 的极坐标方程为
的极坐标方程为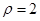 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为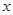 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆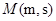 作平行于
作平行于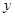 轴的直线
轴的直线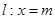 ,设
,设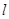 与
与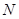 ,向量
,向量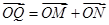 .
.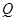 的轨迹方程;
的轨迹方程;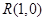 ,求
,求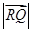 的最小值.
的最小值.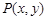 在椭圆
在椭圆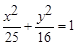 上,若
上,若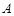 点坐标为
点坐标为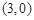 ,
,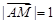 ,且
,且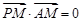 ,则
,则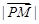 的最小值是( )
的最小值是( )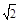
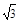
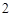

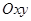 中,若双曲线
中,若双曲线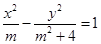 的焦距为8,则
的焦距为8,则