题目内容
已知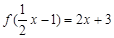 ,
, 则
则 等于 ( )
等于 ( )
A.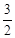 | B.  | C. | D. |
D
解析试题分析:令 ,所以
,所以 ,因为
,因为 所以
所以
 。
。
考点:函数解析式的求法。
点评:用换元法求函数的解析式一定要注意新元的取值范围。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
已知函数 的图象如图所示(其中
的图象如图所示(其中 是函数
是函数 的导函数).下面四个图象中,
的导函数).下面四个图象中,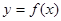 的图象大致是( )
的图象大致是( )

| A. | B. | C. | D. |
定义函数 ,其中
,其中 ,且对于
,且对于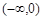 中的任意一个
中的任意一个 都与集合
都与集合 中的
中的 对应,
对应, 中的任意一个
中的任意一个 都与集合
都与集合 中的
中的 对应,则
对应,则 的值为( )
的值为( )
A. | B.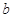 | C.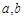 中较小的数 中较小的数 | D.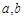 中较大的数 中较大的数 |
根据表格中的数据,可以判断方程 必有一个根在区间( )
必有一个根在区间( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.78 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
B.(0,1)
C.(1,2)
D.(2,3)
函数 的定义域为{0,1,2,3},那么其值域为( )
的定义域为{0,1,2,3},那么其值域为( )
A. | B.{0,1,2,3} |
C. | D. |
函数 的图象如右图所示,下列说法正确的是( )
的图象如右图所示,下列说法正确的是( )
①函数 满足
满足
②函数 满足
满足
③函数 满足
满足
④函数 满足
满足
| A.①② | B.②④ | C.①③ | D.③④ |
定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,当
,当 时,
时,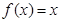 ,则
,则
| A.335 | B.338 | C.1678 | D.2012 |
定义域为R的函数 满足条件:
满足条件:
① ;
;
②
 ; ③
; ③ .
.
则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
函数 的定义域为( )
的定义域为( )
| A.[1,3] | B. | C.(1,3) | D. |