题目内容
（2013•南京二模）在△ABC中，已知AB=2，BC=3，∠ABC=60°，BD⊥AC，D为垂足，则
•
的值为
．
| BD |
| BC |
| 27 |
| 7 |
| 27 |
| 7 |
分析：因为 BD 是 AC 边上的高，所以 BD丄CC，
•
=0，故有
•
=
•（
+
）=
2+
•
=|
|2．由△ABC的面积=
AB×BCsin60°=
AC×BD结合余弦定理能求出 BD的长，从而得出结果．
| BD |
| DC |
| BD |
| BC |
| BD |
| BD |
| DC |
| BD |
| BD |
| DC |
| BD |
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：∵BD是AC边上的高，∴BD丄AC，
∴
•
=0，
∴
•
=
•（
+
）=
2+
•
=|
|2．
又△ABC的面积=
AB×BCsin60°或△ABC的面积=
AC×BD
∴
AB×BCsin60°=
AC×BD
∴
×2×3sin60°=
×BD
∴BD=
∴|
|2=
．
故答案为：
．
∴
| BD |
| DC |
∴
| BD |
| BC |
| BD |
| BD |
| DC |
| BD |
| BD |
| DC |
| BD |
又△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 4+9-2×2×3cos60° |
∴BD=
3
| ||
| 7 |
∴|
| BD |
| 27 |
| 7 |
故答案为：
| 27 |
| 7 |
点评：本题考查平面向量的数量积的运算，是基础题．解题时要认真审题，仔细解答，注意向量垂直的合理运用．
练习册系列答案
相关题目
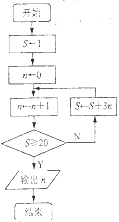（2013•南京二模）如图是一个算法流程图，其输出的n的值是