题目内容
(12分)(2010·山东德州模拟)已知f(x)=(x2+ax+a)e-x(a≤2,x∈R).
(1)当a=1时,求f(x)的单调区间;(2)若f(x)的极大值为4e-2,求出a的值.
【答案】
解:(1)当a=1时,f(x)=(x2+x+1)e-x,f′(x)=e-x(-x2+x),当f′(x)>0时,0<x<1.当f′(x)<0时,x>1或x<0.
∴f(x)的单调递增区间为(0,1),单调递减区间为(-∞,0),(1,+∞).
(2)f′(x)=(2x+a)e-x-e-x(x2+ax+a)=e-x[-x2+(2-a)x].令f′(x)=0,得x=0或x=2-a.列表如下:
由表可知,f(x)极大值=f(2-a)=(4-a)ea-2.
∵4-a=4且a-2=-2,
所以存在实数a=0使f(x)有极大值4e-2.
【解析】略

练习册系列答案
相关题目
(本题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
5 |
0.050 |
|
第2组 |
|
① |
0.350 |
|
第3组 |
|
30 |
② |
|
第4组 |
|
20 |
0.200 |
|
第5组 |
|
10 |
0.100 |
|
合计 |
100 |
1.000 |
|
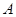 与展馆
与展馆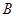 位于观光路的同侧,在观光路上相距
位于观光路的同侧,在观光路上相距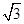 千米的
千米的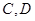 两点分别测得
两点分别测得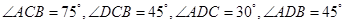 ,(
,(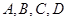 在同一平面内),求展馆
在同一平面内),求展馆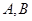 之间的距离.
之间的距离.