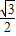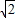题目内容
函数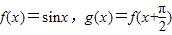
，直线x=t（t∈R）与f（x），g（x）的图象交于M、N两点，则M、N两点间的距离|MN|的最大值是（ ）A．
B．
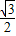
C．
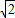
D．2
【答案】分析：由已知中直线x=t分别交函数f（x）、g（x）的图象于M、N两点，构造函数表示M、N的距离，根据辅助角公式可将其化为一个正弦型函数的形式，根据正弦型函数的性质，即可得到答案．
解答：解：由题意可得：
，
所以
．
因为直线x=t（t∈R）与f（x），g（x）的图象交于M、N两点，
所以|MN|=|sinx-cosx|，
所以|sinx-cosx|=|
sin（x-
）|∈[0，
]．
所以M、N两点间的距离|MN|的最大值为
．
故答案为：
．
点评：本题考查的知识点是三角函数的最值，其中构造函数表示M、N的距离，将平面上两动点之间的距离问题转化为三角函数的最值问题，是解答本题的关键．
解答：解：由题意可得：
，所以
．因为直线x=t（t∈R）与f（x），g（x）的图象交于M、N两点，
所以|MN|=|sinx-cosx|，
所以|sinx-cosx|=|
sin（x-）|∈[0，]．所以M、N两点间的距离|MN|的最大值为
．故答案为：
．点评：本题考查的知识点是三角函数的最值，其中构造函数表示M、N的距离，将平面上两动点之间的距离问题转化为三角函数的最值问题，是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
，3），N（
个单位得到函数g（x）图象，直线x=t（t∈[0，
]）与f（x），g（x）的图象分别交于P，Q两点，求|PQ|的最大值．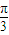
，3），N（
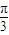，-3）．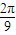
个单位得到函数g（x）图象，直线x=t（t∈[0，
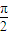]）与f（x），g（x）的图象分别交于P，Q两点，求|PQ|的最大值．
，3），N（
，-3）．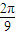
个单位得到函数g（x）图象，直线x=t（t∈[0，
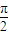]）与f（x），g（x）的图象分别交于P，Q两点，求|PQ|的最大值．
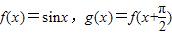，直线x=t（t∈R）与f（x），g（x）的图象交于M、N两点，则M、N两点间的距离|MN|的最大值是（ ）
