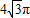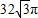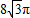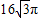题目内容
圆锥侧面展开图是一个半径为12的半圆,则这个圆锥的内切球体积是( )
A.4
| B.32
| C.8
| D.16
|
设圆锥的底面半径是r,
则得到2πr=12π,
解得:r=6,
这个圆锥的底面半径是6.
故圆锥的轴截面是一个等边三角形,其内切圆的半径即为这个圆锥的内切球的半径,
∴这个圆锥的内切球的半径R=2
,
则这个圆锥的内切球体积是
πR3=32
π,
故选B.
则得到2πr=12π,
解得:r=6,
这个圆锥的底面半径是6.
故圆锥的轴截面是一个等边三角形,其内切圆的半径即为这个圆锥的内切球的半径,
∴这个圆锥的内切球的半径R=2
| 3 |
则这个圆锥的内切球体积是
| 4 |
| 3 |
| 3 |
故选B.

练习册系列答案
相关题目