Question

袋中有形状和大小都相同的小球5个，球的编号依次为1、2、3、4、5，从袋中依次取三次球，每次取1个球，取后放回，若每个球被取出的可能性均等，则取出的球的最大号码为3的概率为

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

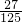
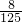
B
分析：根据题意，这是有放回的抽取，先由分步计数原理计算出从袋中依次有放回的取三次球，再用间接法计算取出的球的最大号码为3的情况数目，由古典概型的公式，计算可得答案．
解答：根据题意，从袋中依次有放回的取三次球，有5×5×5=125种情况；
为求出取出的球的最大号码为3的情况数目，用间接法：先算只有1、2、3三个球的情况，再排除其中只有1、2的情况，
则取出的球的最大号码为3的情况有3³-2³=19种；
则其概率为；
故选B．
点评：本题考查古典概率的计算，注意区分题意中“有放回”与“无放回”抽取．