题目内容
(本小题满分12分)
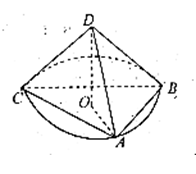
如图,已知四棱锥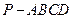 中,侧棱
中,侧棱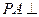 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形,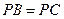 ,
,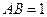 ,
,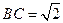 ,
,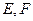 分别是
分别是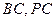 的中点.
的中点.
(1)求证: 平面
平面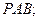
(2)当平面 与底面
与底面 所成二面角为
所成二面角为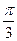 时,求二面角
时,求二面角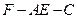 的大小.
的大小.
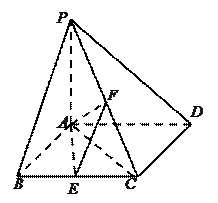
如图,已知四棱锥
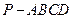 中,侧棱
中,侧棱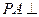 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形,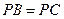 ,
,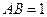 ,
,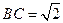 ,
,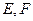 分别是
分别是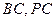 的中点.
的中点.(1)求证:
 平面
平面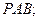
(2)当平面
 与底面
与底面 所成二面角为
所成二面角为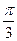 时,求二面角
时,求二面角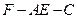 的大小.
的大小.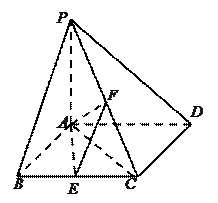
解:
(1)证明:∵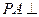 平面
平面 ,∴
,∴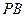 的射影是
的射影是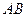 ,
,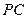 的射影是
的射影是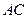 ,
,
∵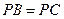 ∴
∴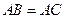 ∴
∴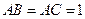 ,且
,且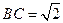 ,
,
∴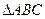 是直角三角形,且
是直角三角形,且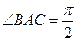 ,…………………………………3分
,…………………………………3分
∴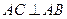 ,∵
,∵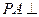 平面
平面 ,∴
,∴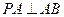 ,
,
且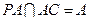 ,∴
,∴ 平面
平面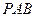 ………………………………………6分
………………………………………6分
(2)解法1:由(1)知
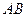 ,且
,且 是平行四边形,可知
是平行四边形,可知
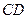 ,
,
又∵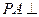 平面
平面 ,由三垂线定理可知,
,由三垂线定理可知,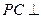
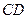 ,
,
又∵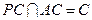 由二面角的平面角的定义可知,
由二面角的平面角的定义可知,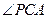 是平面
是平面 与底面
与底面 所成二面角,故
所成二面角,故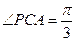 ,故在
,故在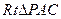 中,
中,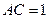 ,∴
,∴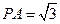 ,
,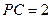 ,
,
从而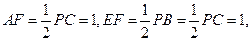 又在
又在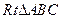 中,
中,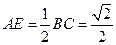 ,
,
∴在等腰三角形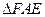 ,分别取
,分别取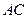 中点
中点 和
和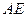 中点
中点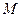 ,连接
,连接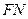 ,
,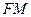 和
和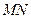 ,
,
∴中位线 ,且
,且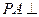 平面
平面 ,∴
,∴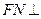 平面
平面 ,
,
在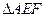 中,中线
中,中线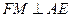 ,由三垂线定理知,
,由三垂线定理知,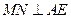 ,
,
 为二面角
为二面角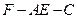 的平面角,
的平面角,
在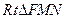 中,
中,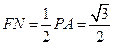 ,
,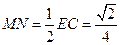 ,
,
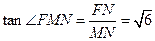 ,
,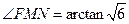 ,
,
∴二面角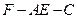 的大小为
的大小为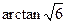 .
.
解法2:由(Ⅰ)知,以点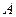 为坐标原点,以
为坐标原点,以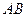 、
、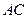 、
、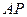
所在的直线分别为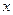 轴、
轴、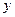 轴、
轴、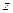 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
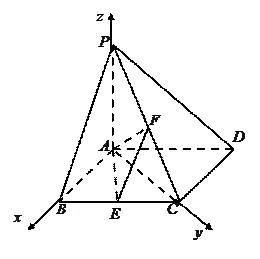
设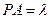 ,则
,则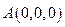 ,
,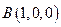 ,
,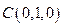 ,
,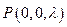 ,
,
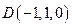 ,
,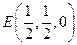 ,
,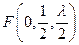 ,
,
则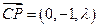 ,
,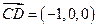 ,
,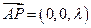
设平面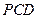 的一个法向量为
的一个法向量为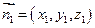 ,
,
则由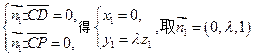
又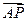 是平面
是平面 的一个法向量,
的一个法向量,
平面 与底面
与底面 所成二面角为
所成二面角为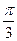
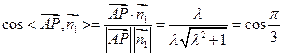 ,解得
,解得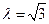 ,
,
设平面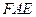 的一个法向量为
的一个法向量为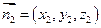 ,
,
则由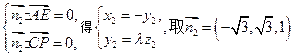 .
.
又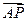 是平面
是平面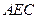 的一个法向量,
的一个法向量,
设二面角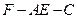 的平面角为
的平面角为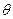 ,则
,则
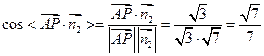 ,∴
,∴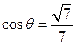 ∴
∴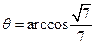
∴二面角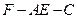 的大小为
的大小为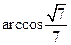 .…………………….…….……12分
.…………………….…….……12分
(1)证明:∵
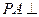 平面
平面 ,∴
,∴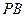 的射影是
的射影是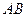 ,
,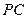 的射影是
的射影是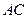 ,
,∵
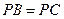 ∴
∴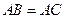 ∴
∴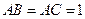 ,且
,且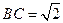 ,
,∴
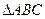 是直角三角形,且
是直角三角形,且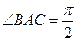 ,…………………………………3分
,…………………………………3分∴
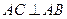 ,∵
,∵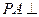 平面
平面 ,∴
,∴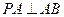 ,
,且
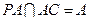 ,∴
,∴ 平面
平面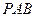 ………………………………………6分
………………………………………6分(2)解法1:由(1)知

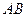 ,且
,且 是平行四边形,可知
是平行四边形,可知
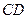 ,
,又∵
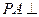 平面
平面 ,由三垂线定理可知,
,由三垂线定理可知,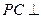
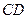 ,
,又∵
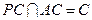 由二面角的平面角的定义可知,
由二面角的平面角的定义可知,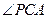 是平面
是平面 与底面
与底面 所成二面角,故
所成二面角,故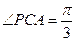 ,故在
,故在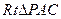 中,
中,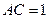 ,∴
,∴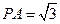 ,
,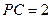 ,
,从而
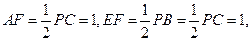 又在
又在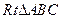 中,
中,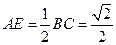 ,
,∴在等腰三角形
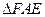 ,分别取
,分别取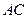 中点
中点 和
和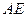 中点
中点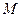 ,连接
,连接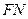 ,
,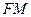 和
和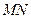 ,
,∴中位线
 ,且
,且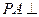 平面
平面 ,∴
,∴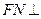 平面
平面 ,
,在
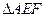 中,中线
中,中线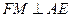 ,由三垂线定理知,
,由三垂线定理知,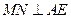 ,
, 为二面角
为二面角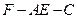 的平面角,
的平面角,在
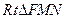 中,
中,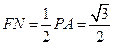 ,
,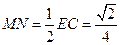 ,
,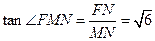 ,
,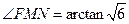 ,
,∴二面角
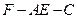 的大小为
的大小为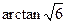 .
.解法2:由(Ⅰ)知,以点
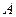 为坐标原点,以
为坐标原点,以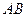 、
、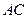 、
、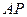
所在的直线分别为
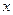 轴、
轴、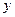 轴、
轴、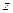 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.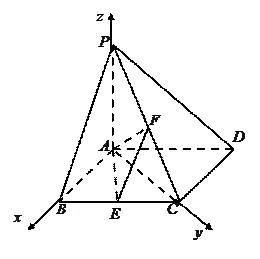
设
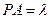 ,则
,则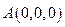 ,
,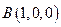 ,
,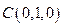 ,
,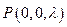 ,
,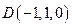 ,
,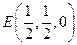 ,
,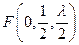 ,
,则
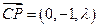 ,
,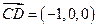 ,
,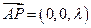
设平面
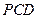 的一个法向量为
的一个法向量为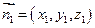 ,
,则由
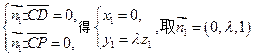
又
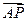 是平面
是平面 的一个法向量,
的一个法向量,平面
 与底面
与底面 所成二面角为
所成二面角为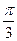
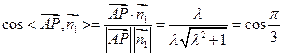 ,解得
,解得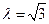 ,
,设平面
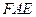 的一个法向量为
的一个法向量为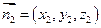 ,
,则由
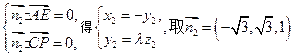 .
.又
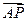 是平面
是平面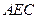 的一个法向量,
的一个法向量,设二面角
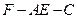 的平面角为
的平面角为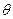 ,则
,则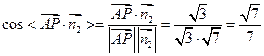 ,∴
,∴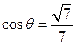 ∴
∴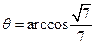
∴二面角
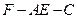 的大小为
的大小为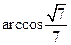 .…………………….…….……12分
.…………………….…….……12分略

练习册系列答案
相关题目
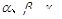 表示三个不同的平面,有下列四个命题:
表示三个不同的平面,有下列四个命题: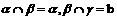 且
且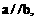 则
则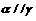 ;
;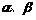 外,
外,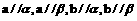 ,则
,则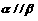 ;
;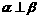 ,
,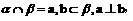 则
则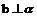 ;
;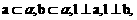 则
则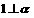 .
.
 (1)(3)
(1)(3)  (2)(4)
(2)(4)  (3)(4)
(3)(4)  (1)(2)
(1)(2)


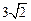 ,且DA,DB,DC两两互相垂直,
,且DA,DB,DC两两互相垂直,