题目内容
已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(-1)=0,且对任意的x∈R,总有f(x)-x≥0,并且当x∈(0,2)时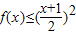 ,求f(x)的解析式.
,求f(x)的解析式.
【答案】分析:由题意可得当x=1时,有1≤f(1)≤1,即f(1)=1,结合f(-1)=0可得 ,进而可得a+c=b=
,进而可得a+c=b= ,又由二次函数的恒成立可得
,又由二次函数的恒成立可得 ,可得
,可得 ,再由基本不等式可得当且只有当a=c=
,再由基本不等式可得当且只有当a=c= 时,满足题意,进而可得解析式.
时,满足题意,进而可得解析式.
解答:解:∵对任意的x∈R,总有f(x)-x≥0,并且当x∈(0,2)时 ,
,
∴当x=1时,有1≤f(1)≤1,即f(1)=1,结合f(-1)=0可得 ,
,
解得a+c=b= ,又∵对于一切实数x,f(x)-x≥0恒成立,
,又∵对于一切实数x,f(x)-x≥0恒成立,
∴ax2+(b-1)x+c≥0(a≠0),对于一切实数x恒成立,
∴ ,即
,即 ,
,
∵a+c= ,且a+c≥2
,且a+c≥2 =
= ,
,
∴当且只有当a=c= 时,不等式成立,
时,不等式成立,
∴f(x)= x2+
x2+ x+
x+
点评:本题考查函数解析式的求解,涉及基本不等式和恒成立问题,属中档题.
 ,进而可得a+c=b=
,进而可得a+c=b= ,又由二次函数的恒成立可得
,又由二次函数的恒成立可得 ,可得
,可得 ,再由基本不等式可得当且只有当a=c=
,再由基本不等式可得当且只有当a=c= 时,满足题意,进而可得解析式.
时,满足题意,进而可得解析式.解答:解:∵对任意的x∈R,总有f(x)-x≥0,并且当x∈(0,2)时
 ,
,∴当x=1时,有1≤f(1)≤1,即f(1)=1,结合f(-1)=0可得
 ,
,解得a+c=b=
 ,又∵对于一切实数x,f(x)-x≥0恒成立,
,又∵对于一切实数x,f(x)-x≥0恒成立,∴ax2+(b-1)x+c≥0(a≠0),对于一切实数x恒成立,
∴
 ,即
,即 ,
,∵a+c=
 ,且a+c≥2
,且a+c≥2 =
= ,
,∴当且只有当a=c=
 时,不等式成立,
时,不等式成立,∴f(x)=
 x2+
x2+ x+
x+
点评:本题考查函数解析式的求解,涉及基本不等式和恒成立问题,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目