题目内容
(本小题满分14分)已知定义域为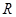 的单调函数
的单调函数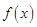 是奇函数,当
是奇函数,当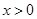 时,
时,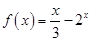 .
.
(I)求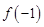 的值;
的值;
(II)求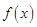 的解析式;
的解析式;
(III)若对任意的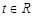 ,不等式
,不等式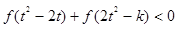 恒成立,求实数
恒成立,求实数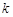 的取值范围.
的取值范围.
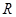 的单调函数
的单调函数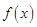 是奇函数,当
是奇函数,当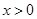 时,
时,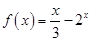 .
.(I)求
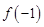 的值;
的值;(II)求
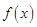 的解析式;
的解析式;(III)若对任意的
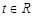 ,不等式
,不等式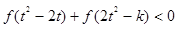 恒成立,求实数
恒成立,求实数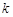 的取值范围.
的取值范围.(1) ;(2)
;(2) ;(3)
;(3) 。
。
 ;(2)
;(2) ;(3)
;(3) 。
。试题分析: (I)因为f(x)是奇函数,所以f(-1)=-f(1)从而问题得解.
(II)因为f(x)为R上的奇函数,所以f(0)=0,然后用-x代替
 中的x,-f(x)代替
中的x,-f(x)代替 中的f(x)再两边同乘以-1可得x<0的解析式.从而可得f(x)在R上的解析式是一个分段函数.
中的f(x)再两边同乘以-1可得x<0的解析式.从而可得f(x)在R上的解析式是一个分段函数.(III) 因为f(x)为定义域为
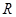 的单调函数,并且由于由于当x
的单调函数,并且由于由于当x >0时,f(x)是
 ,从而可得f(x)在R上是减函数,所以由
,从而可得f(x)在R上是减函数,所以由 得
得 进一步可得
进一步可得 ,所以
,所以 ,然后再转化为一元二次不等式恒成立问题解决即可。
,然后再转化为一元二次不等式恒成立问题解决即可。(1)
 定义域为
定义域为 的函数
的函数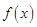 是奇函数 ,所以
是奇函数 ,所以 -------2分
-------2分 (2)
 定义域为
定义域为 的函数
的函数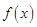 是奇函数
是奇函数  ------------4分
------------4分 当
 时,
时,

又
 函数
函数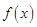 是奇函数
是奇函数 
 ------------7分
------------7分综上所述
 ----8分
----8分(3)
 且
且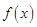 在
在 上单调
上单调 在
在 上单调递减 -------10分
上单调递减 -------10分由
 得
得
 是奇函数
是奇函数 
,又

 是减函数
是减函数 
 ------------12分
------------12分即
 对任意
对任意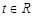 恒成立
恒成立  得
得 即为所求----------------14分
即为所求----------------14分点评:奇函数的图像关于原点对称,因而在求对称区间上的解析式时,可用利用-x,-f(x)分别代替对称区间上解析式中的x,f(x)即可得到所求区间上的解析式.另外奇函数在对称区间上具有相同的单调性,当定义域中有0值时,f(0)=0这些都是奇函数常用的结论,勿必记住.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( ) 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时, ,那么当
,那么当 时,
时,


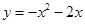
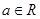 且
且 ,设函数
,设函数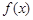 = ax2 +x-3alnx.
= ax2 +x-3alnx.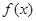 的单调区间;
的单调区间; 对任意
对任意 满足
满足 ,且
,且 ,则
,则 的值为 。
的值为 。  其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 的函数
的函数 ,有下列结论:
,有下列结论: ;②该函数是奇函数;
;②该函数是奇函数; ; ④当
; ④当 时
时 为增函数,当
为增函数,当 时
时
 ,
, ,则从集合
,则从集合 到集合
到集合 的映射最多有 个.
的映射最多有 个.