题目内容
1.如果函数y=sin(2x+ϕ)的图象关于直线x=-$\frac{π}{8}$对称,那么ϕ=kπ+$\frac{3π}{4}$,k∈z.分析 由题意根据正弦函数的图象的对称性可得 2×(-$\frac{π}{8}$)+ϕ=kπ+$\frac{π}{2}$,k∈z,由此求得ϕ的值.
解答 解:∵函数y=sin(2x+ϕ)的图象关于直线x=-$\frac{π}{8}$对称,∴2×(-$\frac{π}{8}$)+ϕ=kπ+$\frac{π}{2}$,k∈z,
即ϕ=kπ+$\frac{3π}{4}$,k∈z,
故答案为:kπ+$\frac{3π}{4}$,k∈z.
点评 本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
12.从装有4粒相同的玻璃球的瓶中,随意倒出若干粒玻璃球(至少1粒),记倒出奇数粒玻璃球的概率为P1,倒出偶数粒玻璃球的概率为P2,则( )
| A. | P1<P2 | B. | P1>P2 | ||
| C. | P1=P2 | D. | P1,P2大小不能确定 |
10.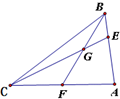 如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
 如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |