题目内容
| ∫ | 2 -2 |
| 4-x2 |
| A、0 | B、π | C、2π | D、2π+4 |
分析:由和的积分等于积分的和展开,前一部分由半圆的面积求得,后一部分直接由微积分基本定理求解.
解答:解:
(
+x)dx
=
dx
xdx.
xdx=
x2
=
×22-
×(-2)2=0,
由y=
,得
,
∴
dx等于以原点为圆心,以2为半径的上半圆的面积,等于
π×22=2π.
∴
(
+x)dx=2π.
故选:C.
| ∫ | 2 -2 |
| 4-x2 |
=
| ∫ | 2 -2 |
| 4-x2 |
| +∫ | 2 -2 |
| ∫ | 2 -2 |
| 1 |
| 2 |
| | | 2 -2 |
| 1 |
| 2 |
| 1 |
| 2 |
由y=
| 4-x2 |
|
∴
| ∫ | 2 -2 |
| 4-x2 |
| 1 |
| 2 |
∴
| ∫ | 2 -2 |
| 4-x2 |
故选:C.
点评:本题考查了定积分,考查了微积分基本定理,是基础的计算题

练习册系列答案
相关题目
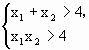 ,所以
,所以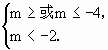 得m≤-4.
得m≤-4. -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0, (x>0),
(x>0), ,又a<0,
,又a<0,