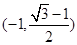题目内容
函数 的值域是
的值域是
- A.[-3,1]
- B.[-1,+∞)
- C.[2,2
 ]
] - D.[1,2
 ]
]
D
分析:由已知中函数的解析式我们根据 =4,结合根式的非负性,我们可设
=4,结合根式的非负性,我们可设 =2sinα,
=2sinα,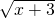 =2cosα(α∈[0,
=2cosα(α∈[0, ]),进而利用和差角公式,将函数的解析式化为正弦型函数的形式,进而得到答案.
]),进而利用和差角公式,将函数的解析式化为正弦型函数的形式,进而得到答案.
解答:∵ =4,
=4,
∴令 =2sinα,
=2sinα,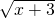 =2cosα(α∈[0,
=2cosα(α∈[0, ]),
]),
∴y=2sinα+2cosα-1
=2 sin(α+
sin(α+ )-1,α∈[0,
)-1,α∈[0, ]
]
∵α+ ∈[
∈[ ,
, ]
]
∴y∈
故选D.
点评:本题考查的知识点是函数的值域,三角换元法,和差角公式及正弦型函数的性质,其中根据已知函数的解析,利用三角换元法,将函数的解析式化为正弦型函数的形式,是解答本题的关键.
分析:由已知中函数的解析式我们根据
 =4,结合根式的非负性,我们可设
=4,结合根式的非负性,我们可设 =2sinα,
=2sinα,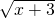 =2cosα(α∈[0,
=2cosα(α∈[0, ]),进而利用和差角公式,将函数的解析式化为正弦型函数的形式,进而得到答案.
]),进而利用和差角公式,将函数的解析式化为正弦型函数的形式,进而得到答案.解答:∵
 =4,
=4,∴令
 =2sinα,
=2sinα,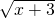 =2cosα(α∈[0,
=2cosα(α∈[0, ]),
]),∴y=2sinα+2cosα-1
=2
 sin(α+
sin(α+ )-1,α∈[0,
)-1,α∈[0, ]
]∵α+
 ∈[
∈[ ,
, ]
]∴y∈

故选D.
点评:本题考查的知识点是函数的值域,三角换元法,和差角公式及正弦型函数的性质,其中根据已知函数的解析,利用三角换元法,将函数的解析式化为正弦型函数的形式,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则函数
,则函数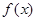 的值域是( ).
的值域是( ).  B.
B.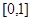 C.
C.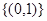 D.
D.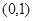
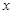 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数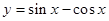 的值域是( )
的值域是( ) B.
B.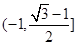 C.
C.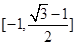 D.
D.