题目内容
已知点P是圆x2+y2=1上的一个动点,过P作PQ⊥x轴于Q,设
(1)求点M的轨迹方程;
(2)求向量![]() 与
与![]() 夹角的最大值,并求此时P点的坐标.
夹角的最大值,并求此时P点的坐标.
解:(1)设P(x0,y0),M(x,y),则![]() =(x0,y0),
=(x0,y0), ![]() =(x0,0),
=(x0,0), ![]() =
= ![]() +
+![]() =(2x0,y0).2分
=(2x0,y0).2分
∴ 化为
化为
∵![]() +
+![]() =1,∴
=1,∴![]() +y2=1.
+y2=1.
(2)设向量![]() 与
与![]() 的夹角为α.
的夹角为α.
则cosα=
= .
.
令t=3x02+1,
则cosα=![]()
![]() =
=![]()
![]() ≥
≥![]() ,
,
当且仅当t=2时,即P点坐标为(±![]() ,±
,±![]() )时,等号成立.
)时,等号成立.
∴![]() 与
与![]() 夹角的最大值是arccos
夹角的最大值是arccos![]() .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
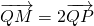 的点M的轨迹为曲线C.
的点M的轨迹为曲线C. 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.