题目内容
已知函数f（x）=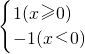
，则不等式x+（x+2）f（x+2）≤4的解集是
- A.{x|-2＜x＜1}
- B.{x|x≤1}
- C.{x|x＜1}
- D.{x|x＜-2}
B
分析：分x+2大于等于0和小于0两种情况考虑，当x+2大于等于0时，f（x+2）=1，代入不等式，即可求出x的范围；当x+2小于0时，f（x+2）=-1，代入不等式，即可求出x的范围，求出两范围的并集即为原不等式的解集．
解答：①当x+2≥0即x≥-2时，
不等式x+（x+2）f（x+2）≤4化为：x+（x+2）×1≤4，
即x≤1，故-2≤x≤1；
②当x+2＜0即x＜-2时，
不等式x+（x+2）f（x+2）≤4化为：x+（x+2）×（-1）≤4，
即-2≤4，这显然成立．
综上可知，原不等式的解集为{x|x≤1}．
故选B
点评：此题考查了其他不等式的解法，考查了分类讨论的数学思想及转化的思想，是一道综合题．
分析：分x+2大于等于0和小于0两种情况考虑，当x+2大于等于0时，f（x+2）=1，代入不等式，即可求出x的范围；当x+2小于0时，f（x+2）=-1，代入不等式，即可求出x的范围，求出两范围的并集即为原不等式的解集．
解答：①当x+2≥0即x≥-2时，
不等式x+（x+2）f（x+2）≤4化为：x+（x+2）×1≤4，
即x≤1，故-2≤x≤1；
②当x+2＜0即x＜-2时，
不等式x+（x+2）f（x+2）≤4化为：x+（x+2）×（-1）≤4，
即-2≤4，这显然成立．
综上可知，原不等式的解集为{x|x≤1}．
故选B
点评：此题考查了其他不等式的解法，考查了分类讨论的数学思想及转化的思想，是一道综合题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|