题目内容
已知三角形ABC的面积是9
,角A,B,C成等差数列,其对应边分别是a,b,c,则a+c的最小值是
| 3 |
12
12
.分析:利用等差数列的性质,结合基本不等式,即可求得a+c的最小值.
解答:解:由题意可得:2B=A+C,又A+B+C=π,解得B=
∵△ABC的面积为
acsinB=
×
ac=9
∴ac=36
a+c≥2
=12
当且仅当a=c时取等号
∴a+c的最小值是12
故答案为:12
| π |
| 3 |
∵△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴ac=36
a+c≥2
| ac |
当且仅当a=c时取等号
∴a+c的最小值是12
故答案为:12
点评:本题考查等差数列的性质,考查基本不等式的运用,正确运用等差数列的性质是关键.

练习册系列答案
相关题目
 如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.
如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.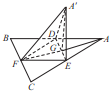 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ),顶点C在
),顶点C在 轴
轴 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面