题目内容
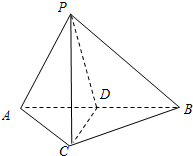
7. 如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.
如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.(Ⅰ)求证:AM⊥平面PBC;
(Ⅱ)求二面角A-PC-B的余弦值;
(Ⅲ)证明:在线段PC上存在点D,使得BD⊥AC,并求$\frac{PD}{PC}$的值.
分析 (Ⅰ)根据线面垂直的判定定理即可证明AM⊥平面PBC;
(Ⅱ)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角A-PC-B的余弦值;
(Ⅲ)根据向量关系,以及直线垂直,利向量法进行求解即可.
解答 证明:(Ⅰ)因为PA⊥平面ABC,BC?平面ABC,
所以PA⊥BC.
因为BC⊥AB,PA∩AB=A,
所以BC⊥平面PAB.又AM?平面PAB,
所以AM⊥BC.
因为PA=AB,M为PB的中点,
所以AM⊥PB.
又PB∩BC=B,
所以AM⊥平面PBC.
(Ⅱ)如图,在平面ABC内,作AZ∥BC,则AP,AB,AZ两两互相垂直,
建立空间直角坐标系A-xyz.
则A(0,0,0),P(2,0,0),B(0,2,0),C(0,2,2),M(1,1,0).
$\overrightarrow{AP}=(2,0,0)$,$\overrightarrow{AC}=(0,2,2)$,$\overrightarrow{AM}=(1,1,0)$
设平面APC的法向量为$\overrightarrow{n}=(x,y,z)$,则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AP}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$
即$\left\{\begin{array}{l}{x=0}\\{2y+2z=0}\end{array}\right.$
令y=1,则z=-1.
所以$\overrightarrow{n}$=(0,1,-1).
由(Ⅰ)可知$\overrightarrow{AM}$=(1,1,0)为平面的法向量,
设$\overrightarrow{n}$,$\overrightarrow{AM}$的夹角为α,则cosα=$\frac{1}{2}$.
因为二面角A-PC-B为锐角,
所以二面角A-PC-B的余弦值为$\frac{1}{2}$.
(Ⅲ)设D(u,v,w)是线段PC上一点,且$\overrightarrow{PD}=λ\overrightarrow{PC}$,(0≤λ≤1).
即(u-2,v,w)=λ(-2,2,2).
所以u=2-2λ,v=2λ,w=2λ.
所以$\overrightarrow{BD}=(2-2λ,2λ-2,2λ)$.
由$\overrightarrow{BD}•\overrightarrow{AC}=0$,得$λ=\frac{1}{2}$.
因为$\frac{1}{2}∈[0,1]$,
所以在线段PC存在点D,使得BD⊥AC.
此时$\frac{PD}{PC}$=$λ=\frac{1}{2}$.
点评 本题主要考查空间位置关系的判断,以及利用向量法求二面角的大小以及空间线面垂直的判定,考查学生的推理能力.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | $\sqrt{3}$x-y-4=0 | B. | $\sqrt{3}$x-y-4$\sqrt{3}$=0 | C. | $\sqrt{3}$x+y-4=0 | D. | $\sqrt{3}$x+y-4$\sqrt{3}$=0 |
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{1+\sqrt{10}}$ |
 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.