题目内容
(2013•和平区二模)若直线y=x+m与曲线y=3-
有公共点,则m所的取值范围是( )
| x(4-x) |
分析:先求出曲线y=3-
的定义域,同时将曲线进行等价转化为半圆,然后利用直线与圆的位置关系进行判断求值.
| x(4-x) |
解答:解:由x(4-x)≥0,得0≤x≤4.由y=3-
得(y-3)2=x(4-x)=-x2+4x,且y≤3.
即(x-2)2+(y-3)2=4,因为0≤x≤4,所以曲线为圆心为(2,3),半径为2的下半圆.
圆心到直线距离d=
=
,由
≤2,解得1-2
≤m≤1+2
.
因为圆是下半圆,所以当直线y=x+m经过点(0,3)时,m取到最大值3,所以1-2
≤m≤3.即m所的取值范围是[1-2
,3].

故选B.
| x(4-x) |
即(x-2)2+(y-3)2=4,因为0≤x≤4,所以曲线为圆心为(2,3),半径为2的下半圆.
圆心到直线距离d=
| |2-3+m| | ||
|
| |m-1| | ||
|
| |m-1| | ||
|
| 2 |
| 2 |
因为圆是下半圆,所以当直线y=x+m经过点(0,3)时,m取到最大值3,所以1-2
| 2 |
| 2 |

故选B.
点评:本题考查直线与圆的位置关系的应用.本题在对曲线进行等价化简时,要注意取值的等价性,如果不注意隐含条件,本题很容易会把曲线看成整圆,而导致出错是个出错.本题容易错选A答案.

练习册系列答案
相关题目
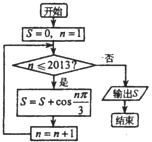 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )