题目内容
已知函数y=f（x）满足：f（1）=a（0＜a≤1），且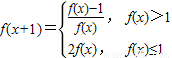
则f（2）= （用a表示），若
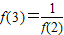，则a= ．
【答案】分析：由函数y=f（x）满足：f（1）=a（0＜a≤1），且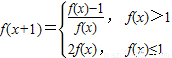
，知f（2）=f（1+1）=2f（1）=2a；由
=
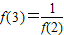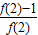，知f（2）=2a=2，由此能求出a．
解答：解：∵函数y=f（x）满足：f（1）=a（0＜a≤1），
且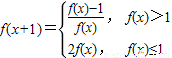
，
∴f（2）=f（1+1）=2f（1）=2a；
∵
=
，
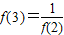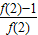∴f（2）=2a=2，
∴a=1．
故答案为：2a，1．
点评：本题考查函数值的求法，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
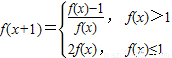，知f（2）=f（1+1）=2f（1）=2a；由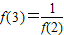=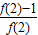，知f（2）=2a=2，由此能求出a．解答：解：∵函数y=f（x）满足：f（1）=a（0＜a≤1），
且
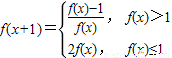，∴f（2）=f（1+1）=2f（1）=2a；
∵
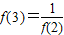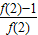=，∴f（2）=2a=2，
∴a=1．
故答案为：2a，1．
点评：本题考查函数值的求法，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，当x＞0 时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]≤0 的解集为
已知函数y=f（x）的图象如图，则满足