Question

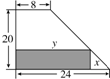某厂有形状为直角梯形的边角料，现从中截取矩形铁片（如图示），当矩形面积最大时，矩形的两边x，y分别应为

15，12

．

Answer 1

分析：以直角梯形的下底直角边端点为原点，两直角边方向为x，y轴建立直角坐标系，由直角三角形相似，确定x，y之间的关系，表示出矩形的面积，即可求得结论．

解答：解：以直角梯形的下底直角边端点为原点，两直角边方向为x，y轴建立直角坐标系，过点D作DE⊥x轴于点E，
∵NH∥DE，
∴△CNH∽△CDE，
∴

CH

CE

=

NH

DE

，
∵CH=24-y，CE=24-8，DE=OA=20，NH=x，
∴

24-y

24-8

=

x

20

，得x=

5

4

•（24-y），
∴矩形面积S=xy=-

5

4

（y-12）²+180，
∴当y=12时，S有最大值，此时x=15．
故答案为：15，12．

点评：本题考查的是直角梯形以及矩形的性质的相关知识点，考查配方法的运用，属于中档题．