题目内容
【题目】已知曲线![]() 所围成封闭图形面积为
所围成封闭图形面积为![]() ,曲线
,曲线![]() 是以曲线
是以曲线![]() 与坐标轴的交点为顶点的椭圆, 离心率为
与坐标轴的交点为顶点的椭圆, 离心率为![]() . 平面上的动点
. 平面上的动点![]() 为椭圆
为椭圆![]() 外一点,且过
外一点,且过![]() 点
点
引椭圆![]() 的两条切线互相垂直.
的两条切线互相垂直.
(1)求曲线![]() 的方程;
的方程;
(2)求动点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)利用![]() 和离心率为
和离心率为![]() 得到关于
得到关于![]() 的方程组,进而求出曲线的方程;(2)设出直线方程,与椭圆方程联立,得到关于
的方程组,进而求出曲线的方程;(2)设出直线方程,与椭圆方程联立,得到关于![]() 的一元二次方程,利用判别式、根与系数的关系及两直线垂直进行求解.
的一元二次方程,利用判别式、根与系数的关系及两直线垂直进行求解.
试题解析:(1)因为![]() 所围成封闭图形面积
所围成封闭图形面积![]()
椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,解得
,解得![]() , 得
, 得![]()
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,当两切线
,当两切线![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设
时,设![]() 的方程为
的方程为![]() ,
,
联立直线![]() 和椭圆
和椭圆![]() 的方程,得
的方程,得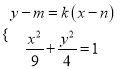 ,消去
,消去![]() 并整理,得:
并整理,得:
![]()
因为直线![]() 和椭圆
和椭圆![]() 有且仅有一个交点,
有且仅有一个交点, ![]()
![]() ,
,
化简并整理,得![]() .*
.*
同理直线![]() 的斜率
的斜率![]() 满足方程*,又因为两切线
满足方程*,又因为两切线![]() 垂直,所以两切线斜率之积
垂直,所以两切线斜率之积![]() .
.![]() ,
, ![]() . ①
. ①
当切线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 的斜率不存在,此时
的斜率不存在,此时![]() ,符合①式.
,符合①式.
综上所述,点![]() 的轨迹方程为
的轨迹方程为![]() .
.

练习册系列答案
相关题目
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).