Question

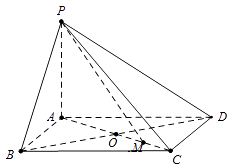
【题目】如图，四边形PDCE为矩形，四边形ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD= CD=a，PD= a．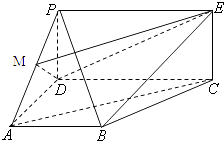
（1）若M为PA中点，求证：AC∥平面MDE；
（2）求平面PAD与PBC所成锐二面角的大小．

Answer 1

【答案】
（1）解：证明：连接PC，交DE与N，连接MN，

在△PAC中，∵M，N分别为两腰PA，PC的中点

∴MN∥AC，

又AC面MDE，MN面MDE，

所以 AC∥平面MDE

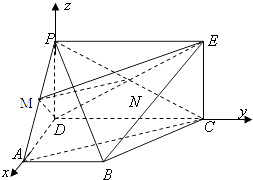
（2）解：以D为空间坐标系的原点，分别以 DA，DC，DP所在直线为x，y，z轴建立空间直角坐标系，

则P（0，0， a），B（a，a，0），C（0，2a，0），

所以 ， ，

设平面PAD的单位法向量为 ，则可取

设面PBC的法向量 ，

则有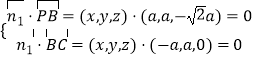

即： ，取z=1，

则 ∴

设平面PAD与平面PBC所成锐二面角的大小为θ，

∴

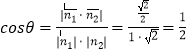
∴θ=60°，

所以平面PAD与平面PBC所成锐二面角的大小为60°

【解析】（1）连接PC，交DE与N，连接MN，所以MN∥AC，再根据线面平行的判定定理可得答案．（2）以D为空间坐标系的原点，分别以 DA，DC，DP所在直线为x，y，z轴建立空间直角坐标系，分别求出两个平面的法向量，再求出两个向量的夹角，进而转化为二面角的平面角．