题目内容

用数学归纳法证明

分析：本题考查数学归纳法在证明等式中的应用.

用数学归纳法证明一个与正整数有关的命题，关键是第二步，要注意当n=k+1时，等式两边的式子与n=k时等式两边的式子的联系，增加了哪些项，减少了哪些项，问题就会顺利解决.

证明：（1）当n=1时，左边=，

右边=,等式成立.

(2)假设当n=k时，等式成立，即

则当n=k+1时，

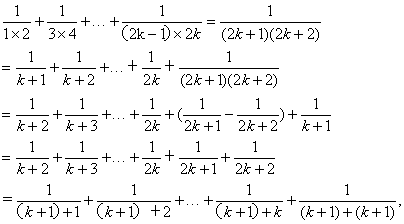
即当n=k+1时，等式成立.

根据（1）、（2）可知，对一切n∈N*，等式成立.

点评：解题过程中容易将n=k+1时，等式右边错写为，从而导致证明错误或无法进行.特别要注意等式右边的每一个式子都在随n的变化而变化.

练习册系列答案
相关题目
已知a＞0，b＞0，n＞1，n∈N*．用数学归纳法证明：
an+bn
2
≥(
a+b
2
)n．
已知m，n为正整数．
（Ⅰ）用数学归纳法证明：当x＞-1时，（1+x）m≥1+mx；
（Ⅱ）对于n≥6，已知(1-
1
n+3
)n＜
1
2
，求证(1-
m
n+3
)n＜(
1
2
)m，m=1，2…，n；
（Ⅲ）求出满足等式3n+4n+5n+…+（n+2）n=（n+3）n的所有正整数n．
用数学归纳法证明贝努利（Bernoulli）不等式：如果x是实数，且x＞-1，x≠0，n为大于1的自然数，那么有（1+x）n＞1+nx．
已知：函数f(x)=-
1
6
x3+
1
2
x2+x，x∈R．
（Ⅰ）求证：函数f（x）的图象关于点A(1，
4
3
)中心对称，并求f（-2007）+f（-2006）+…+f（0）+f（1）+…+f（2009）的值．
（Ⅱ）设g（x）=f′（x），an+1=g（an），n∈N+，且1＜a1＜2，求证：
（ⅰ）请用数学归纳法证明：当n≥2时，1＜an＜
3
2
；
（ⅱ）|a1-
2
|+|a2-
2
|+…+|an-
2
|＜2．
用数学归纳法证明：（cosα+isinα）n=cosnα+isinnα，（其中i为虚数单位）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网