题目内容
如图2-2-9所示，AB、CD都是圆的弦，且AB∥CD，F为圆上一点，延长FD、AB交于点E.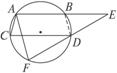
图2-2-9
求证：AE·AC=AF·DE.
思路分析:连结BD，则BD=AC，即证AE·BD=AF·DE.
证明:连结BD，∵AB∥CD，
∴BD=AC.
∵A、B、D、F四点共圆，∴∠EBD=∠F.
∵∠E为△EBD和△EFA的公共角，
∴△EBD∽△EFA.∴
.
∴
，即AE·AC=AF·DE
练习册系列答案
孟建平名校考卷系列答案
相关题目
孟建平名校考卷系列答案
=a，
=b，
=c，则
等于( )
AB.