题目内容
在斜△ABC中，| c |
| b |
| b |
| c |
| tanA |
| tanB |
| tanA |
| tanC |
分析：利用余弦定理化简条件可得3（b2+c2 ）=4a2，化简要求的式子为
，把正弦定理、余弦定理代入
化简求得结果．
| sin2A |
| cosAsinBsinC |
化简求得结果．
解答：解：在斜△ABC中，
+
=8cosA，故
=8
，化简可得 3（b2+c2 ）=4a2．
故
+
=
+
=
=
=
=
=
=
=6，
故答案为：6．
| c |
| b |
| b |
| c |
| c2+b2 |
| bc |
| c2+b2-a2 |
| 2bc |
故
| tanA |
| tanB |
| tanA |
| tanC |
| sinAcosB |
| cosAsinB |
| sinAcosC |
| cosAsinC |
| sinAcosBsinC+sinBsinAcosC |
| cosAsinBsinC |
| sinAsin(B+C) |
| cosAsinBsinC |
=
| sin2A |
| cosAsinBsinC |
| a2 | ||
|
| 2a2 |
| b2+c2- a2 |
| 2a2 | ||
|
故答案为：6．
点评：本题考查正弦定理、余弦定理的应用，式子的变形是解题的难点和关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
（2012•梅州二模）如图，已知斜三棱柱ABC-A1B1C1中，点B1在底面ABC上的射影落在BC上，CA=CB=a，AB=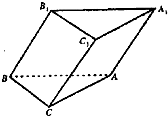
如图，已知斜三棱柱ABC-A1B1C1中，点B1在底面ABC上的射影落在BC上，CA=CB=a，AB=
．
．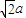