Question

【题目】如图，四棱锥中，，，为中点.

（1）证明：平面；

（2）若平面，是边长为2的正三角形，求点到平面的距离.

Answer 1

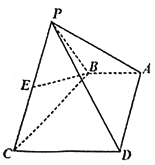
【答案】（1）见解析.（2）.

【解析】分析：第一问首先在平面内寻找的平行线，这个任务借助中位线，从而取中点，即为所求，之后应用线面平行的判定定理证得结果；第二问利用线面平行将点到平面的距离转化为求点到平面的距离，之后用等级法，借助于三棱锥的体积和三棱锥的体积相等求得对应的高，即点到面的距离.

详解：（1）证明：取的中点，连结

∵为的中点，∴，且

又∵，且

∴，且，故四边形为平行四边形

∴

又平面，平面，

∴平面.

（2）由（1）得平面

故点到平面的距离等于点到平面的距离

取的中点，连结

∵平面，平面，

∴平面平面

又是边长为2的正三角形

∴，，且

∵平面平面

∴平面，

∵四边形是直角梯形，

∴

∵，，，

∴，

∴

记点到平面的距离为，

∵三棱锥的体积

∴.

∴点到平面的距离为.