题目内容
已知一个等差数列{an}前10项的和是 ,前20项的和是
,前20项的和是
(1)求这个等差数列的前n项和Sn.
(2)求使得Sn最大的序号n的值.
解:(1)设等差数列{an}的公差为d,由已知S10= ,S20=
,S20= .
.
由等差数列的求和公式可得:S10=10a1+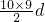 =
= ①
①
S20=20a1+ =
= ②,由①②解得d=
②,由①②解得d=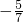 ,a1=5
,a1=5
故an=5+(n-1)(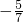 )=
)= ,
,
所以前n项和Sn=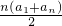 =
=
(2)由(1)可知,an= ,令
,令 解得n≥8,
解得n≥8,
故差数列{an}的前7项均为正,第8项为0,从第9项开始全为负值,
故差数列{an}的前7项和等于前8项和都为最大值.
故使得Sn最大的序号n的值为:7或8
分析:(1)设等差数列{an}的公差为d,由已知建立方程组可解d和a1,代公式可求Sn;
(2)由(1)可知数列的通项公式,可得等差数列{an}的前7项均为正,第8项为0,从第9项开始全为负值,故可得答案.
点评:本题为等差数列的求和问题以及和的最值问题,从数列自身的变化来求解最值会使问题变得简单,属基础题.
 ,S20=
,S20= .
.由等差数列的求和公式可得:S10=10a1+
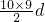 =
= ①
①S20=20a1+
 =
= ②,由①②解得d=
②,由①②解得d=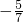 ,a1=5
,a1=5故an=5+(n-1)(
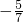 )=
)= ,
,所以前n项和Sn=
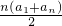 =
=
(2)由(1)可知,an=
 ,令
,令 解得n≥8,
解得n≥8,故差数列{an}的前7项均为正,第8项为0,从第9项开始全为负值,
故差数列{an}的前7项和等于前8项和都为最大值.
故使得Sn最大的序号n的值为:7或8
分析:(1)设等差数列{an}的公差为d,由已知建立方程组可解d和a1,代公式可求Sn;
(2)由(1)可知数列的通项公式,可得等差数列{an}的前7项均为正,第8项为0,从第9项开始全为负值,故可得答案.
点评:本题为等差数列的求和问题以及和的最值问题,从数列自身的变化来求解最值会使问题变得简单,属基础题.

练习册系列答案
相关题目
已知一个等差数列共有2n+1项,其中奇数项之和为290,偶数项之和为261,则第n+1项为( )
| A、30 | B、29 | C、28 | D、27 |
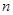 项和为286,则项数
项和为286,则项数