题目内容
已知m∈R,函数f(x)=(x2+mx+m)·ex.(1)若函数f(x)没有零点,求实数m的取值范围;
(2)若函数f(x)存在极大值,并记为g(m),求g(m)的表达式;
(3)当m=0时,求证:f(x)≥x2+x3.
解:(1)令f(x)=0,得(x2+mx+m)·ex=0,∴x2+mx+m=0.∵函数f(x)没有零点,∴Δ=m2-4m<0.
∴0<m<4.
(2)f′(x)=(2x+m)ex+(x2+mx+m)ex=(x+2)(x+m)ex,
令f′(x)=0,得x=-2或-m,
当m>2时,则-m<-2,
x | (-∞,-m) | -m | (-m,-2) | -2 | (-2,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | me-m | ↘ | (4-m)e-2 | ↗ |
当x=-m时,f(x)取得极大值me-m,
当m=2时,f′(x)=(x+2)2ex≥0,f(x)在R上为增函数,∴f(x)无极大值.
当m<2时,则-m>-2.
x | (-∞,-2) | -2 | (-m,-2) | -m | (-m,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | (4-m)e-2 | ↘ | me-m | ↗ |
当x=-2时,f(x)取得极大值(4-m)e-2,
∴g(m)=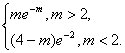
(3)证明:令φ(x)=ex-1-x,则φ′(x)=ex-1,
当x>0时,φ′(x)>0,φ(x)为增函数;当x<0时,φ′(x)<0,φ(x)为减函数,
∴当x=0时,φ(x)取得最小值0.
∴φ(x)≥φ(0)=0.∴ex-1-x≥0.∴ex≥1+x.∴x2ex≥x2+x3.∴f(x)≥x2+x3.

练习册系列答案
相关题目