题目内容
设F1,F2分别是双曲线x2-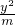 =1的左右焦点,过点F2作与x轴垂直的直线和双曲线的一个交点为A,且满足|
=1的左右焦点,过点F2作与x轴垂直的直线和双曲线的一个交点为A,且满足|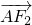 |=|
|=|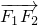 |,则双曲线的离心率为
|,则双曲线的离心率为
- A.

- B.

- C.

- D.不确定,与m取值有关
C
分析:利用双曲线的定义可求得|AF1|-|AF2|=(2 -2)
-2) =2,可求得c,继而可求得双曲线的离心率.
=2,可求得c,继而可求得双曲线的离心率.
解答:∵双曲线方程为x2-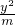 =1,
=1,
∴a=1,c= ,
,
又AF2与x轴垂直,|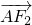 |=|
|=|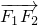 |,
|,
∴△AF1F2是以AF1为斜边的等腰直角三角形,
∴|AF1|= ×2c=2
×2c=2
 ,
,
∴|AF1|-|AF2|=(2 -2)
-2) =2a=2,
=2a=2,
∴ =
= +1,即c=
+1,即c= +1,
+1,
∴双曲线的离心率e= =
= +1.
+1.
故选C.
点评:本题考查双曲线的简单性质,求得m的值是关键,属于中档题.
分析:利用双曲线的定义可求得|AF1|-|AF2|=(2
 -2)
-2) =2,可求得c,继而可求得双曲线的离心率.
=2,可求得c,继而可求得双曲线的离心率.解答:∵双曲线方程为x2-
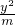 =1,
=1,∴a=1,c=
 ,
,又AF2与x轴垂直,|
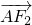 |=|
|=|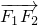 |,
|,∴△AF1F2是以AF1为斜边的等腰直角三角形,
∴|AF1|=
 ×2c=2
×2c=2
 ,
,∴|AF1|-|AF2|=(2
 -2)
-2) =2a=2,
=2a=2,∴
 =
= +1,即c=
+1,即c= +1,
+1,∴双曲线的离心率e=
 =
= +1.
+1.故选C.
点评:本题考查双曲线的简单性质,求得m的值是关键,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目