题目内容
 已知正方形ABCD的边长为2,在正方形及其内部任选一点P(在正方形及其内部点的选取都是等可能的),作PM⊥AB于M,PN⊥AD于N,矩形PMAN的面积为S.
已知正方形ABCD的边长为2,在正方形及其内部任选一点P(在正方形及其内部点的选取都是等可能的),作PM⊥AB于M,PN⊥AD于N,矩形PMAN的面积为S.(1)请建立适当的坐标系,设P(x,y),写出x,y满足的条件,并作出满足S≤1的P点的区域;
(2)求S≤1的概率.
分析:(1)分别以AB、AD为x轴、y轴,建立直角坐标系.根据矩形的面积公式得P坐标为(x,y)时,S=xy≤1对应的区域在曲线y=
的下方、且在正方形内部的部分.由此可得相应的不等式组并作出图形如图所示.
(2)根据定积分的几何意义,利用积分计算公式算出阴影部分面积为ln4+1,结合正方形ABCD的面积为4利用几何概型计算公式,即可算出S≤1的概率.
| 1 |
| x |
(2)根据定积分的几何意义,利用积分计算公式算出阴影部分面积为ln4+1,结合正方形ABCD的面积为4利用几何概型计算公式,即可算出S≤1的概率.
解答:解:(1)以直线AB为x轴,AD为y轴,A为坐标原点建立直角坐标系.-------(1分)
∵点P(x,y)在正方形及其内部,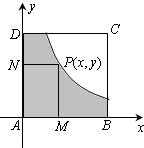
∴S=xy(0≤x≤2,0≤y≤2).-----------(3分)
故满足满足S≤1的P(x,y)点满足的条件是
-----------(5分)
P点的区域如右图所示.-----------------------(7分)
(2)P点所在的区域面积为
S=2
dx+1×1=2(lnx)
+1=2ln2+1=ln4+1,-------(12分)
∵正方形ABCD的面积为S'=4,
∴满足S≤1的概率为P=
=
.------------------(14分)
∵点P(x,y)在正方形及其内部,

∴S=xy(0≤x≤2,0≤y≤2).-----------(3分)
故满足满足S≤1的P(x,y)点满足的条件是
|
P点的区域如右图所示.-----------------------(7分)
(2)P点所在的区域面积为
S=2
| ∫ | 2 1 |
| 1 |
| x |
| | | 2 1 |
∵正方形ABCD的面积为S'=4,
∴满足S≤1的概率为P=
| S |
| S′ |
| ln4+1 |
| 4 |
点评:本题着重考查了不等式组表示的平面区域、定积分的几何意义与积分计算公式和几何概型计算公式等知识,属于中档题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.