题目内容
已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则当x∈[-4,4]时不等式x?f′(x)<0的解集为( )
| A、(-2,0)∪(2,4) | B、(-4,-2)∪(0,2) | C、(-2,0) | D、(0,2) |
分析:根据条件求出函数的周期性,利用函数的奇偶性周期性和单调性之间的关系得到函数f(x)的草图,然后讨论x的符号,根据函数单调性和导数之间的关系即可得到结论.
解答:解:由f(x-4)=-f(x)得f(x-8)=-f(x-4)=-[-f(x)]=f(x),
即函数的周期是8.
∵函数f(x)是奇函数,
∴f(x-4)=-f(x)=f(-x),
即函数关于
=-2对称.
∴f(0)=0,f(-4)=-f(0)=0,f(4)=0.
∵在区间[0,2]上f(x)是增函数,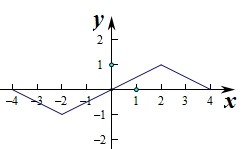
∴f(x)在[-2,2]上是增函数,在[2,4]上是减函数,在[-4,-2]上是减函数.
作出函数的草图如图:
若x=0时,不等式x•f′(x)<0不成立.
若x>0,则不等式x•f′(x)<0等价为f′(x)<0,此时函数单调递减,由图象可知,此时2<x<4.
若x<0,则不等式x•f′(x)<0等价为f′(x)>0,此时函数单调递增,由图象可知,此时-2<x<0,
故不等式x•f′(x)<0的解集为(-2,0)∪(2,4).
故选:A.
即函数的周期是8.
∵函数f(x)是奇函数,
∴f(x-4)=-f(x)=f(-x),
即函数关于
| x-4-x |
| 2 |
∴f(0)=0,f(-4)=-f(0)=0,f(4)=0.
∵在区间[0,2]上f(x)是增函数,

∴f(x)在[-2,2]上是增函数,在[2,4]上是减函数,在[-4,-2]上是减函数.
作出函数的草图如图:
若x=0时,不等式x•f′(x)<0不成立.
若x>0,则不等式x•f′(x)<0等价为f′(x)<0,此时函数单调递减,由图象可知,此时2<x<4.
若x<0,则不等式x•f′(x)<0等价为f′(x)>0,此时函数单调递增,由图象可知,此时-2<x<0,
故不等式x•f′(x)<0的解集为(-2,0)∪(2,4).
故选:A.
点评:本题主要考查函数周期性,奇偶性和单调性之间的关系,利用函数单调性和导数之间的关系即可得到结论.综合考查了函数性质的综合应用.

练习册系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)
 时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.
时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.