题目内容
选作题(请在下列2小题中选做一题,全做的只计算第(1)题得分)
(1)圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-4sinθ,则经过两圆圆心的直线的直角坐标方程为
(2)若不等式|3x-b|<4的解集中的整数有且仅有0,1,2,则b的取值范围是
(1)圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-4sinθ,则经过两圆圆心的直线的直角坐标方程为
x-y-2=0
x-y-2=0
.(2)若不等式|3x-b|<4的解集中的整数有且仅有0,1,2,则b的取值范围是
(2,4)
(2,4)
.分析:(1)把 圆O1和圆O2的极坐标方程化为直角坐标方程,求出两个圆的圆心坐标,用截距式求出经过两圆圆心的直线的直角坐标方程,并化为一般式.
(2)由不等式|3x-b|<4可得
<x<
,由题意可得-1≤
<0,且 2<
≤3,由此求得b的取值范围.
(2)由不等式|3x-b|<4可得
| b-4 |
| 3 |
| 4+b |
| 3 |
| b-4 |
| 3 |
| 4+b |
| 3 |
解答:解:(1)∵圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-4sinθ,故它们的直角坐标方程为 x2+y2=4x x2+y2=-4y,
故圆心坐标分别为(2,0)、(0,-2),故经过两圆圆心的直线的直角坐标方程为
+
=1,即 x-y-2=0.
故答案为 x-y-2=0.
(2)由不等式|3x-b|<4可得
<x<
.
再由解集中的整数有且仅有0,1,2,可得-1≤
<0,且 2<
≤3.
解得-1≤b<4,且 2<b≤5,故有2<b<4,
故b的取值范围是(2,4),
故答案为 (2,4).
故圆心坐标分别为(2,0)、(0,-2),故经过两圆圆心的直线的直角坐标方程为
| x |
| 2 |
| y |
| -2 |
故答案为 x-y-2=0.
(2)由不等式|3x-b|<4可得
| b-4 |
| 3 |
| 4+b |
| 3 |
再由解集中的整数有且仅有0,1,2,可得-1≤
| b-4 |
| 3 |
| 4+b |
| 3 |
解得-1≤b<4,且 2<b≤5,故有2<b<4,
故b的取值范围是(2,4),
故答案为 (2,4).
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,绝对值不等式的解法,属于中档题.

练习册系列答案
相关题目
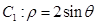 ,曲线
,曲线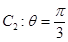 ,若曲线C1与C2交于
,若曲线C1与C2交于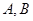 两点,则线段
两点,则线段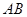 的长度为
的长度为
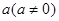 和
和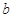 ,不等式
,不等式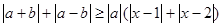 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.