题目内容
(本小题12分)如图,已知椭圆
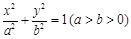 的长轴为
的长轴为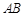 ,过点
,过点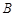 的直线
的直线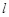 与
与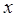 轴垂直.直线
轴垂直.直线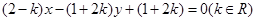 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率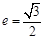 。
。
(1)求椭圆的标准方程;
(2)设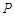 是椭圆上异于
是椭圆上异于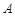 、
、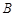 的任意一点,
的任意一点,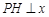 轴,
轴,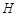 为垂足,延长
为垂足,延长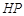 到点
到点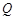 使得
使得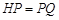 ,连结
,连结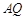 延长交直线
延长交直线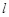 于点
于点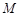 ,
,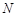 为
为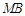 的中点.试判断直线
的中点.试判断直线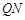 与以
与以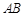 为直径的圆
为直径的圆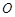 的位置关系。
的位置关系。
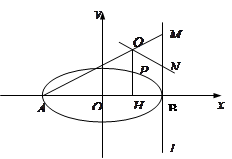

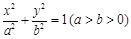 的长轴为
的长轴为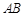 ,过点
,过点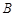 的直线
的直线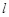 与
与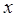 轴垂直.直线
轴垂直.直线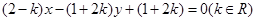 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率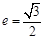 。
。(1)求椭圆的标准方程;
(2)设
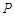 是椭圆上异于
是椭圆上异于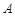 、
、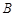 的任意一点,
的任意一点,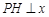 轴,
轴,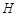 为垂足,延长
为垂足,延长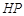 到点
到点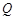 使得
使得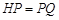 ,连结
,连结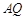 延长交直线
延长交直线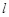 于点
于点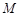 ,
,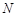 为
为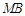 的中点.试判断直线
的中点.试判断直线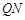 与以
与以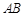 为直径的圆
为直径的圆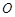 的位置关系。
的位置关系。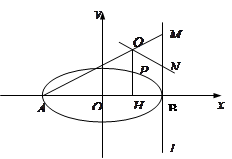
解:(1)将 整理得
整理得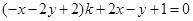
解方程组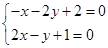 得直线所经过的定点(0,1),所以
得直线所经过的定点(0,1),所以 .
.
由离心率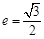 得
得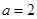 .
.
所以椭圆的标准方程为 .
.
(2)设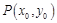 ,则
,则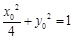 .
.
∵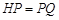 ,∴
,∴ .∴
.∴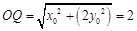
∴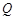 点在以
点在以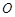 为圆心,2为半径的的圆上.即
为圆心,2为半径的的圆上.即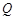 点在
点在
以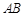 为直径的圆
为直径的圆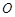 上.
上.
又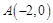 ,∴直线
,∴直线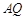 的方程为
的方程为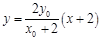 .
.
令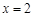 ,得
,得 .又
.又 ,
,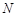 为
为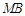 的中点,∴
的中点,∴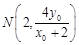 .
.
∴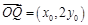 ,
,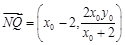 .
.
∴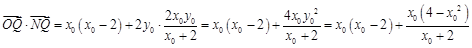
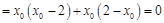 .
.
∴ .∴直线
.∴直线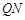 与圆
与圆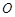 相切.
相切.
 整理得
整理得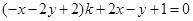
解方程组
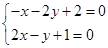 得直线所经过的定点(0,1),所以
得直线所经过的定点(0,1),所以 .
.由离心率
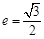 得
得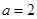 .
.所以椭圆的标准方程为
 .
.(2)设
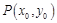 ,则
,则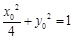 .
.∵
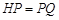 ,∴
,∴ .∴
.∴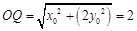
∴
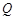 点在以
点在以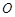 为圆心,2为半径的的圆上.即
为圆心,2为半径的的圆上.即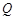 点在
点在以
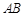 为直径的圆
为直径的圆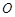 上.
上.又
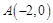 ,∴直线
,∴直线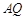 的方程为
的方程为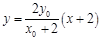 .
.令
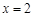 ,得
,得 .又
.又 ,
,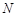 为
为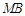 的中点,∴
的中点,∴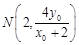 .
.∴
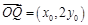 ,
,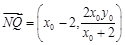 .
.∴
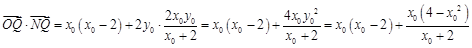
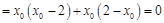 .
.∴
 .∴直线
.∴直线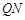 与圆
与圆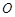 相切.
相切.略

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
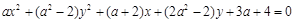 表示圆,则
表示圆,则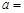 ___________。
___________。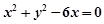 过点(4,2)的最短弦所在直线的斜率为
过点(4,2)的最短弦所在直线的斜率为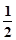

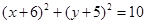
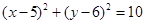

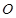 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为 ,点
,点 的极坐标为
的极坐标为 ,若直线
,若直线 过点
过点 ,圆
,圆 以
以 为半径。
为半径。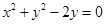 .在以原点为极点,
.在以原点为极点,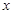 轴正半轴为极轴的极坐标系中,该圆的方程为( )
轴正半轴为极轴的极坐标系中,该圆的方程为( )
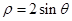
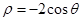
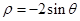

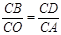 。
。