题目内容
将函数y=
-
（x∈[0，2]）的图象绕坐标原点逆时针旋转θ（θ为锐角），若所得曲线仍是一个函数的图象，则θ的最大值为______．
| -x2+2x+3 |
| 3 |
设f（x）=
-
，根据二次函数的单调性，可得
函数在[0，1]上为增函数，在[1，2]上为减函数．
设函数在 x=0 处，切线斜率为k，则k=f'（0）
∵f'（x）=
•
=
，
∴k=f'（0）=
=tan30°，可得切线的倾斜角为 30°，
因此，要使旋转后的图象仍为一个函数的图象，
旋转θ后的切线倾斜角最多为 90°，
也就是说，最大旋转角为 90°-30°=60°，即θ的最大值为60°
故答案为：60°
| -x2+2x+3 |
| 3 |
函数在[0，1]上为增函数，在[1，2]上为减函数．
设函数在 x=0 处，切线斜率为k，则k=f'（0）
∵f'（x）=
| 1 |
| 2 |
| (-x2 +2x)′ | ||
|
| -x +1 | ||
|
∴k=f'（0）=
| ||
| 3 |
因此，要使旋转后的图象仍为一个函数的图象，
旋转θ后的切线倾斜角最多为 90°，
也就是说，最大旋转角为 90°-30°=60°，即θ的最大值为60°
故答案为：60°
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
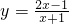作适当的变形利用图象的平移作出它的图象，并写出该函数的值域；
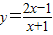作适当的变形利用图象的平移作出它的图象，并写出该函数的值域；