题目内容
设f(x) 是定义在R上的减函数,满足f(x+y)=f(x)·f(y)且f(0)=1,数列{an} 满足
a1=4, (n∈N*);
(n∈N*);
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Sn是数列{an}的前n项和, 试比较Sn与6n2-2的大小。
a1=4,
 (n∈N*);
(n∈N*);(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Sn是数列{an}的前n项和, 试比较Sn与6n2-2的大小。
解:(Ⅰ)由题设知 可化为
可化为
 ,
,
∵y=f(x)是定义在R上的单调减函数,
∴ ,即
,即 ,
,
∴数列 是以
是以 为首项,1为公差的等差数列,
为首项,1为公差的等差数列,
∴ ,
,
即an= 。
。
(Ⅱ)Sn=a1+a2+a3+···+an =4(1+31+32+···+3n-1)=2(3n-1) ,
当n=1时,有Sn=6n2-2=4;
当n=2时,有Sn=16<6n2-2=22;
当n=3时,有Sn=6n2-2=52;
当n=4时,有Sn=160>6n2-2=94;
当n=5时,有Sn=484>6n2-2=148。
由此猜想当n≥4时, 有Sn>6n2-2 3n-1>n2,
3n-1>n2,
下面用数学归纳法证明:
①当n=1时显然成立;
②假设当n=k(k≥4,k∈N*)时, 有3k-1>k2;
当n=k+1时,有3k=3·3k-1>3k2,
∵k≥4,
∴k(k-1)≥12, ∴3k2-(k-1)2=2k(k-1)-1>0即3k2>(k+1)2,
∴3k>3k2>(k+1)2, ∴3k>(k+1)2,因此当n=k+1时原式成立。
由①②可知,当n≥4时有3n-1>n2,
即Sn>6n2-2,
综上可知当n=1,3时,有Sn=6n2-2;当n=2时,有Sn<6n2-2;当n≥4时,有Sn>6n2-2。
 可化为
可化为 ,
,∵y=f(x)是定义在R上的单调减函数,
∴
 ,即
,即 ,
,∴数列
 是以
是以 为首项,1为公差的等差数列,
为首项,1为公差的等差数列, ∴
 ,
,即an=
 。
。(Ⅱ)Sn=a1+a2+a3+···+an =4(1+31+32+···+3n-1)=2(3n-1) ,
当n=1时,有Sn=6n2-2=4;
当n=2时,有Sn=16<6n2-2=22;
当n=3时,有Sn=6n2-2=52;
当n=4时,有Sn=160>6n2-2=94;
当n=5时,有Sn=484>6n2-2=148。
由此猜想当n≥4时, 有Sn>6n2-2
 3n-1>n2,
3n-1>n2,下面用数学归纳法证明:
①当n=1时显然成立;
②假设当n=k(k≥4,k∈N*)时, 有3k-1>k2;
当n=k+1时,有3k=3·3k-1>3k2,
∵k≥4,
∴k(k-1)≥12, ∴3k2-(k-1)2=2k(k-1)-1>0即3k2>(k+1)2,
∴3k>3k2>(k+1)2, ∴3k>(k+1)2,因此当n=k+1时原式成立。
由①②可知,当n≥4时有3n-1>n2,
即Sn>6n2-2,
综上可知当n=1,3时,有Sn=6n2-2;当n=2时,有Sn<6n2-2;当n≥4时,有Sn>6n2-2。

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 >0.
>0. )<f(x-
)<f(x- );
); ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f(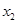 ),则(0,
),则(0, f(
f( 为含峰区间:
为含峰区间: ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r: 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)