题目内容
设集合M={(x,y)|y=2x-1},N={(x,y)|y=ax2-ax+a},是否存在非零整数a,使得M∩N
思路分析:探索特称命题“存在非零整数a,使M∩N![]()
![]() ”的真假,由条件找出a的值.
”的真假,由条件找出a的值.
解:∵M∩N![]()
![]() ,
,
∴M∩N≠![]() ,?
,?
即方程组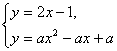 有解,消去y,
有解,消去y,
得ax2-(a+2)x+a+1=0.?
∵a≠0,
∴Δ≥0,即(a+2)2-4a(a+1)≥0.?
解得-![]() ≤a≤
≤a≤![]() ,?
,?
又a∈Z,∴a=-1,1,
即存在非零整数a=-1或1,使得M∩N![]()
![]() .(证明略)?
.(证明略)?
思维启示:对“M∩N![]()
![]() ”进行等价转化“-
”进行等价转化“-![]() ≤a≤
≤a≤![]() ,
,
即找出a的值使命题为真命题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,求a的取值范围。
,求a的取值范围。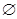 ,求a的取值范围。
,求a的取值范围。