题目内容
(本题满分14分)本题共有2个小题,第一个小题满分6分,第2个小题满分8分。
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]()
(1)证明:![]() 是等比数列;
是等比数列;
(2)求数列![]() 的通项公式,并求出使得
的通项公式,并求出使得![]() 成立的最小正整数
成立的最小正整数![]() .
.
解析:(1) 当n=1时,a1=-14;当n≥2时,an=Sn-Sn-1=-5an+5an-1+1,所以![]() ,
,
又a1-1=-15≠0,所以数列{an-1}是等比数列;
(2) 由(1)知:![]() ,得
,得![]() ,从而
,从而![]() (nÎN*);
(nÎN*);
由Sn+1>Sn,得![]() ,
,![]() ,最小正整数n=15.
,最小正整数n=15.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本) 年销售量.
年销售量. 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;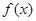 =
=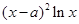 ,
,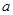 ∈R
∈R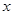 =
=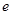 为
为 的极值点,求实数
的极值点,求实数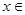 (0,3
(0,3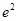 成立.
成立.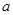 元,每期利率为
元,每期利率为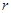 ,设存期为
,设存期为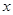 ,本利和(本金加上利息)为
,本利和(本金加上利息)为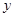 元。
元。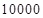 元,每期利率为
元,每期利率为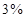 ,试计算
,试计算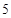 期后的本利和。
期后的本利和。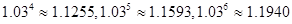 )
) 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
,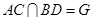 .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求证:
;(Ⅱ)求证: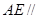 平面
平面 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥 的体积.
的体积.