题目内容
已知数列{an}和{bn}满足a1=2,an-1=an(an+1-1),bn=an-1,n∈N*.求数列{bn}的通项公式.
解:由bn=an-1得an=bn+1代入an-1=an(an+1-1)得bn=(bn+1)bn+1,整理得bn-bn+1=bnbn+1,
∵bn≠0否则an=1,与a1=2矛盾,从而得 ,
,
∵b1=a1-1=1
∴数列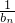 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
∴ ,即
,即 .
.
分析:由题设条件推出bn-bn+1=bnbn+1,bn≠0否则an=1,与a1=2矛盾,从而得 ,所以
,所以 ,由此可知
,由此可知 .
.
点评:本题考查数列的求和公式,解题时要认真审题,仔细解答.
∵bn≠0否则an=1,与a1=2矛盾,从而得
 ,
,∵b1=a1-1=1
∴数列
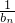 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列∴
 ,即
,即 .
.分析:由题设条件推出bn-bn+1=bnbn+1,bn≠0否则an=1,与a1=2矛盾,从而得
 ,所以
,所以 ,由此可知
,由此可知 .
.点评:本题考查数列的求和公式,解题时要认真审题,仔细解答.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目