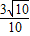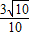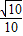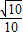题目内容
已知θ是第二象限角,且满足|sin
|=-sin
,则
是( )
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
分析:根据所给的角是一个第二象限的角,写出用集合形式表示的角的范围,求出角的一半的表示形式,根据k的取值看出角的象限,再根据绝对值的意义看出具体位置.
解答:解:∵θ是第二象限角,
∴θ∈(2kπ+
,2kπ+π) k∈z
∴
∈(kπ+
,kπ+
) k∈z
∴
在第一和第三象限,
∵满足|sin
|=-sin
,
∴
在第三象限,
故选C.
∴θ∈(2kπ+
| π |
| 2 |
∴
| θ |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴
| θ |
| 2 |
∵满足|sin
| θ |
| 2 |
| θ |
| 2 |
∴
| θ |
| 2 |
故选C.
点评:本题考查象限角和三角函数的符号,本题解题的关键是求出角的表示形式,进而写出半角的表示形式,注意要对于角的表示形式中出现的K的值分成奇偶两种情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 是第二象限角,
是第二象限角, ,则
,则 = .
= .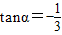 ,则cosα=( )
,则cosα=( )