题目内容
已知变量x，y满足约束条件
则z=2x+y的最大值为
|
2
2
．分析：先根据约束条件画出可行域，再利用几何意义求最值，z=2x+y表示直线在y轴上的截距，只需求出可行域直线在y轴上的截距最大值即可．
解答：
解：作图可行域如图，
易知可行域为一个三角形，
其三个顶点为（0，1），（1，0），（-1，-2），
验证知在点（1，0）时取得最大值2
即当直线z=2x+y过点A（1，0）时，z最大是2，
故答案为2．
解：作图可行域如图，易知可行域为一个三角形，
其三个顶点为（0，1），（1，0），（-1，-2），
验证知在点（1，0）时取得最大值2
即当直线z=2x+y过点A（1，0）时，z最大是2，
故答案为2．
点评：一般在求目标函数的最值时，常用角点法，就是求出可行域的几个拐点，分别代入目标函数，即可求出目标函数的最值．
练习册系列答案
相关题目
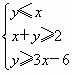，则目标函数Z＝2x＋y的最大值为________．
则目标函数
的最大值为（ ）