题目内容
如图，在矩形
中，点
分别在线段
上，且满足
,若
,则
（ ）
A． | B． | C． | D．1 |
B
解析试题分析：
，
又因为
，所以
，两等式相加得：
.
考点：1、向量的加法；2、平面向量基本定理.
练习册系列答案
阅读快车系列答案
相关题目
已知平面向量
，
，则向量
（ ）
A． | B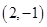． | C． | D． |
已知
是
的重心，点
是
内一点，若
，则
的取值范围是（ ）
A． | B． | C． | D． |
设平面向量
，
，则
( )
A． | B． | C． | D． |
已知向量
，若
，则
等于( )
A． | B． | C． | D． |
在
中，
是
边的中点，角
的对边分别是
，若
，则的形状为( )
| A．直角三角形 | B．钝角三角形 |
| C．等边三角形 | D．等腰三角形但不是等边三角形 |
已知
，
，
，若
与
共线，则
等于 （ ）
| A．5 | B．1 | C． | D． |
向量
,向量，
则
的最大值，最小值分别是( ）
A． | B． | C． | D． |
设向量a＝
，向量b＝
，且a∥b，则锐角θ为( )．
| A．60° | B．30° | C．75° | D．45° |