题目内容
(本小题满分10分)
在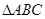 中,已知角
中,已知角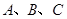 所对的边分别是
所对的边分别是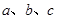 ,边
,边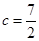 ,
,
且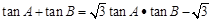 ,又
,又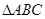 的面积为
的面积为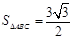 ,求
,求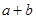 的值。
的值。
在
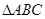 中,已知角
中,已知角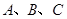 所对的边分别是
所对的边分别是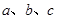 ,边
,边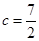 ,
,且
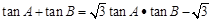 ,又
,又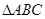 的面积为
的面积为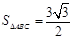 ,求
,求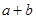 的值。
的值。a+b=

本试题主要是考查了解三角形和两角和差公式的综合运用。
先根据已知化简得到tan(A+B)= ,所以C=
,所以C= ,然后利用正弦面积公式得到△ABC的面积为S△ABC=
,然后利用正弦面积公式得到△ABC的面积为S△ABC= ,∴
,∴ absinC=
absinC= 即
即 ab×
ab× =
= ,得到ab=6,再结合余弦定理得到a+b=
,得到ab=6,再结合余弦定理得到a+b= 。
。
解:由tA.nA.+tA.nB= tA.nA.·tA.nB-
tA.nA.·tA.nB- 可得
可得 =-
=- ,
,
即tA.n(A.+B)=- ∴tA.n(π-C)= -
∴tA.n(π-C)= - , ∴-tA.nC=-
, ∴-tA.nC=- ,
,
∴tA.nC= ∵C∈(0, π), ∴C=
∵C∈(0, π), ∴C=
又△A.BC的面积为S△A.BC= ,∴
,∴ A.bsinC=
A.bsinC= 即
即 A.b×
A.b× =
= , ∴A.b=6
, ∴A.b=6
又由余弦定理可得c2=A.2+b2-2A.bcosC
∴( )2= A.2+b2-2A.bcos
)2= A.2+b2-2A.bcos ∴(
∴( )2= A.2+b2-A.b=(A.+b)2-3A.b∴(A.+b)2=
)2= A.2+b2-A.b=(A.+b)2-3A.b∴(A.+b)2= ,
,
∵A.+b>0, ∴a+b=
先根据已知化简得到tan(A+B)=
 ,所以C=
,所以C= ,然后利用正弦面积公式得到△ABC的面积为S△ABC=
,然后利用正弦面积公式得到△ABC的面积为S△ABC= ,∴
,∴ absinC=
absinC= 即
即 ab×
ab× =
= ,得到ab=6,再结合余弦定理得到a+b=
,得到ab=6,再结合余弦定理得到a+b= 。
。解:由tA.nA.+tA.nB=
 tA.nA.·tA.nB-
tA.nA.·tA.nB- 可得
可得 =-
=- ,
,即tA.n(A.+B)=-
 ∴tA.n(π-C)= -
∴tA.n(π-C)= - , ∴-tA.nC=-
, ∴-tA.nC=- ,
, ∴tA.nC=
 ∵C∈(0, π), ∴C=
∵C∈(0, π), ∴C=
又△A.BC的面积为S△A.BC=
 ,∴
,∴ A.bsinC=
A.bsinC= 即
即 A.b×
A.b× =
= , ∴A.b=6
, ∴A.b=6又由余弦定理可得c2=A.2+b2-2A.bcosC
∴(
 )2= A.2+b2-2A.bcos
)2= A.2+b2-2A.bcos ∴(
∴( )2= A.2+b2-A.b=(A.+b)2-3A.b∴(A.+b)2=
)2= A.2+b2-A.b=(A.+b)2-3A.b∴(A.+b)2= ,
, ∵A.+b>0, ∴a+b=


练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 中,三个内角
中,三个内角 所对的边分别是
所对的边分别是 已知
已知 的面积等于
的面积等于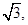 则
则
 中,
中, 则
则
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,求
,求
 ,则∠C =
,则∠C = ,则A的取值范围是( )
,则A的取值范围是( )



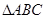 中,如果
中,如果 ,那么角
,那么角 等于 ( )
等于 ( )


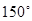
 中,
中, 是
是 和
和 的等差中项,则内角B的取值范围是_____.
的等差中项,则内角B的取值范围是_____.